[题目]某企业需要建造一个容积为8立方米.深度为2米的无盖长方体水池.已知池壁的造价为每平方米100元.池底造价为每平方米300元.设水池底面一边长为米.水池总造价为元.求关于的函数关系式.并求出水池的最低造价. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某企业需要建造一个容积为8立方米，深度为2米的无盖长方体水池，已知池壁的造价为每平方米100元，池底造价为每平方米300元，设水池底面一边长为米，水池总造价为元，求关于的函数关系式，并求出水池的最低造价.

【答案】，最低造价为2800元

【解析】

根据已知条件可设底面一边长为米，则另一边长为米，蓄水池的总造价为，再由均值不等式求得最值即可.

由于长方体蓄水池的容积为8立方米，深为2米，

因此其底面积为4平方米，

设底面一边长为米，则另一边长为米，

又因为池壁的造价为每平方米100元，

而池壁的面积为平方米，

因此池壁的总造价为，

而池底的造价为每平方米300元，池底的面积为4平方米，因此池底的总造价为1200元，

故蓄水池的总造价为.

由函数

当且仅当，即时，函数有最小值，此时总造价最低.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表：

年份	2010	2011	2012	2013	2014
时间代号	1	2	3	4	5
储蓄存款 (千亿元)	6	7	8	9	10

(1)求关于的回归方程；

(2)用所求回归方程预测该地区2015年的人民币储蓄存款.

附：回归方程中，，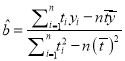

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=是奇函数，g（x）=log2（2x+1）-bx是偶函数．

（1）求a-b；

（2）若对任意的t∈[-1，2]，不等式f（t2-2t-1）+f（2t2-k）＜0恒成立，求实数k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在正方体ABCD-A1B1C1D1中．

（I）求证：AC⊥BD1；

（Ⅱ）是否存在直线与直线AA1，CC1，BD1都相交？若存在，请你在图中画出两条满足条件的直线（不必说明画法及理由）；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数与的图像上存在关于轴对称的点，则的取值范围是________。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在△ABC中，内角A、B、C所对的边分别为a、b、c，已知a≠b，cos2A﹣cos2B= sinAcosA﹣ sinBcosB．（Ⅰ）求角C的大小；
（Ⅱ）若c= ，siniA= ，求△ABC的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C： + =1（0＜b＜3）的左右焦点分别为E，F，过点F作直线交椭圆C于A，B两点，若且
（1）求椭圆C的方程；
（2）已知点O为原点，圆D：（x﹣3）2+y2=r2（r＞0）与椭圆C交于M，N两点，点P为椭圆C上一动点，若直线PM，PN与x轴分别交于点R，S，求证：|OR||OS|为常数．