
(Ⅰ)设函数![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)设正数![]() 满足
满足![]() ,证明
,证明
![]() .
.
(Ⅰ)解:对函数f(x)求导数:
f′(x)=(xlog2x) ′+[(1-x)log2(1-x)] ′
=log2x- log2(1-x)+![]()
= log2x- log2(1-x).
于是f′(![]() )=0.
)=0.
当x<![]() 时,f′(x)=log2x-log2(1-x)<0,f(x)在区间(0,
时,f′(x)=log2x-log2(1-x)<0,f(x)在区间(0,![]() )是减函数,
)是减函数,
当x>![]() 时,f′(x)=log2x-log2(1-x)>0, f(x)在区间(
时,f′(x)=log2x-log2(1-x)>0, f(x)在区间(![]() ,1)是增函数。
,1)是增函数。
所以f(x)在x=![]() 时取得最小值,f(
时取得最小值,f(![]() )=-1.
)=-1.
(Ⅱ)证法一:用数学归纳法证明。
(i)当n=1时,由(Ⅰ)知命题成立。
(ii)假定当n=k时命题成立,即若正数p1,p2,…,![]() 满足p1+p2+…+
满足p1+p2+…+![]() =1,则
=1,则
p1log2p1+p2log2p2+…+![]() log2
log2![]() ≥-k.
≥-k.
当n=k+1时,若正数p1,p2,…, ![]() 满足p1+p2+…+
满足p1+p2+…+![]() =1,令
=1,令
x=p1+p2+…+![]() ,q1=
,q1=![]() q2=
q2=![]() …,
…,![]() =
=![]()
则q1,q2,…,![]() 为正数,且q1+q2+…+
为正数,且q1+q2+…+![]() =1.
=1.
由归纳假定知q1log2q1+q2log2q2+…+![]() log2
log2![]() ≥-k.
≥-k.
p1log2p1+p2log2p2+…+![]() log2
log2![]() =x(q1log2q1+q2log2q2+…+
=x(q1log2q1+q2log2q2+…+![]() log2
log2![]() +log2x)
+log2x)
≥x(-k)+xlog2x, ①
同理,由![]() +
+![]() +…
+…![]() =1-x,可得
=1-x,可得
![]() log2
log2![]() +…+
+…+![]() log2
log2![]()
≥(1-x)(-k)+(1-x)log2(1-x). ②
综合①、②两式
p1log2p1+p2log2p2+…+![]() log2
log2![]()
≥[x+(1-x)](-k)+xlog2x+(1-x)log2(1-x)
≥-(k+1).
即当n=k+1时命题也成立。
根据(i)、(ii)可知对一切正整数n命题成立。
证法二:
令函数g(x)=xlog2x+(c-x)log2(c-x)(常数c>0,x∈(0,c)),那么
g(x)=c[![]() log2
log2![]() +(1-
+(1-![]() )log2(1-
)log2(1-![]() )+log2c],
)+log2c],
利用(Ⅰ)知,当![]() =
=![]() (即x=
(即x=![]() )时,函数g(x)取得最小值。
)时,函数g(x)取得最小值。
于是对任意x1>0,x2>0,都有
x1log2x1+x2log2x2≥2?![]() log2
log2![]()
=(x1+x2)[log2(x1+x2) -1] ①
下面用数学归纳法证明结论.
(i) 当n=1时,由(Ⅰ)知命题成立。
(ii) 设当n=k时命题成立,即若正数p1,p2,…![]() 满足p1+p2+…+
满足p1+p2+…+![]() =1,有
=1,有
p1log2p1+p2log2p2+…+![]() log2
log2![]() ≥-k.
≥-k.
当n=k+1时,p1,p2,…![]() 满足p1+p2+…
满足p1+p2+…![]() =1.
=1.
令H=p1log2p1+p2log2p2+…+![]() log2
log2![]() +
+![]() log2
log2![]() ,由①得到
,由①得到
H≥(p1+p2)[log2(p1+p2) -1]+…+(![]() +
+![]() )[log2(
)[log2(![]() +
+![]() )-1],
)-1],
因为(p1+p2)+…+(![]() +
+![]() )=1,
)=1,
由归纳法假设
(p1+p2)log2(p1+p2)+…+(![]() +
+![]() )log2(
)log2(![]() +
+![]() )≥-k,得到
)≥-k,得到
H≥-k-(p1+p2+…+![]() +
+![]() )=-(k+1).
)=-(k+1).
即当n=k+1时命题也成立。
所以对一切正整数n命题成立。


科目:高中数学 来源:2013届辽宁省分校高三12月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在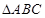 中,
中,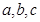 分别为内角
分别为内角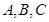 的对边,且
的对边,且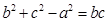 。
。
(Ⅰ)求角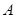 的大小;
的大小;
(Ⅱ)设函数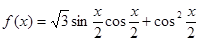 ,求
,求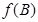 的最大值,并判断此时
的最大值,并判断此时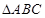 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考文科数学试卷(解析版) 题型:解答题
(本小题满分13分)
已知空间向量 ,
, ,
, ·
· =
= ,
, ∈(0,
∈(0, ).
).
(1)求 及
及 ,
, 的值;
的值;
(2)设函数 ,求
,求 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;
(3)求函数 在区间
在区间 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com