
 )=
)= ,则cos(α+
,则cos(α+ )的值为( )
)的值为( )



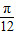 )小于0,然后根据sin(α+
)小于0,然后根据sin(α+ )的值利用同角三角函数间的基本关系求出cos(α+
)的值利用同角三角函数间的基本关系求出cos(α+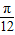 )的值,把所求式子中的α+
)的值,把所求式子中的α+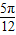 变为(α+
变为(α+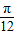 )+
)+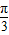 ,然后两角和的余弦函数公式及特殊角的三角函数值化简后,将cos(α+
,然后两角和的余弦函数公式及特殊角的三角函数值化简后,将cos(α+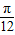 )的值代入即可求出值.
)的值代入即可求出值.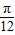 )=
)= ,∴cos(α+
,∴cos(α+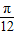 )=-
)=-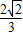 ,
,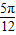 )=cos[(α+
)=cos[(α+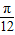 )+
)+ ]
] )cos
)cos -sin(α+
-sin(α+ )sin
)sin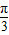
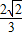 )•
)• -
- •
•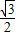
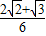 .
.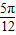 变为(α+
变为(α+ )+
)+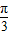 .
. 

 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com