
已知双曲线的中心在原点,离心率为2,一个焦点为F(-2,0).
(1)求双曲线方程;
(2)设Q是双曲线上一点,且过点F,Q的直线l与y轴交于点M,若 = 2
= 2 ,求直线l的方程.
,求直线l的方程.
科目:高中数学 来源: 题型:解答题
如图,椭圆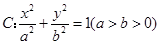 经过点P(1.
经过点P(1. ),离心率e=
),离心率e= ,直线l的方程为x=4.
,直线l的方程为x=4.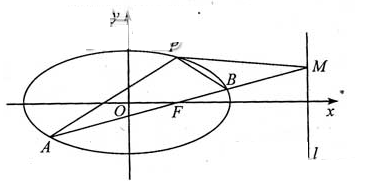
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为 .问:是否存在常数λ,使得
.问:是否存在常数λ,使得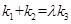 ?若存在,求λ的值;若不存在,说明理由.
?若存在,求λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知圆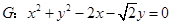 ,经过椭圆
,经过椭圆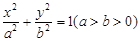 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点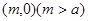 倾斜角为
倾斜角为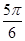 的直线
的直线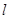 交椭圆于C,D两点,
交椭圆于C,D两点,
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线 的方程为
的方程为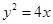 ,过原点作斜率为
,过原点作斜率为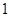 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为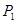 ,过
,过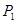 作斜率为
作斜率为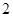 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为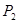 ,过
,过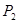 作斜率为
作斜率为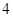 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为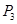 ,如此下去,一般地,过点
,如此下去,一般地,过点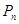 作斜率为
作斜率为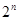 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为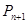 ,设点
,设点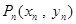 (
(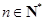 ).
).
(1)指出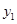 ,并求
,并求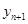 与
与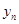 的关系式(
的关系式(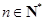 );
);
(2)求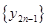 (
(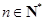 )的通项公式,并指出点列
)的通项公式,并指出点列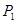 ,
,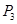 , ,
, ,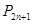 , 向哪一点无限接近?说明理由;
, 向哪一点无限接近?说明理由;
(3)令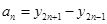 ,数列
,数列 的前
的前 项和为
项和为 ,设
,设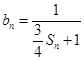 ,求所有可能的乘积
,求所有可能的乘积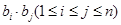 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知椭圆 的左、右焦点分别
的左、右焦点分别
为 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为 的正三角形.
的正三角形.
(1)求椭圆 的方程;
的方程;
(2)过点 任作一动直线
任作一动直线 交椭圆
交椭圆 于
于 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线 运动时,点
运动时,点 在某一定直线上运动,求出该定直线的方程.
在某一定直线上运动,求出该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆于
交椭圆于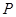 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点.试问直线
两点.试问直线 、
、 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: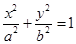 (a>b>0),过点(0,1),且离心率为
(a>b>0),过点(0,1),且离心率为 .
.
(1)求椭圆C的方程;
(2)A,B为椭圆C的左右顶点,直线l:x=2 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时, 恒为定值.
恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,点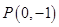 是椭圆
是椭圆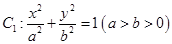 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径, 、
、 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 交圆
交圆 于
于 、
、 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C的中心在原点,一个焦点F(-2,0),且长轴长与短轴长的比为 ,
,
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,设点P是椭圆上的任意一点,若当 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com