练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某电脑公司在甲、乙两地各有一个分公司,甲分公司现有电脑6台,乙分公司现有同一型号的电脑12台.现A地某单位向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台.已知从甲地运往A,B两地每台电脑的运费分别是40元和30元,从乙地运往A,B两地每台电脑的运费分别是80元和50元. 若总运费不超过1000元,则调运方案的种数为

    A．1 B．2

    C．3 D．4

    【答案】C

    【解析】设甲地调运x台电脑至B地,则剩下(6-x)台电脑调运至A地；乙地应调运(8-x)台电脑至B地,运往A地12-(8-x)=(x+4)台电脑().

    则总运费,∴.

    若y≤1000,则,得x≤2.又,∴,∴x=0,1,2,即能有3种调运方案.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝|x－1|＋|x＋1|(x∈R)．

    (1)证明：函数f(x)是偶函数；

    (2)利用绝对值及分段函数知识，将函数解析式写成分段函数的形式，然后画出函数图象；

    (3)写出函数的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设p:实数x满足,其中,命题实数满足

    |x-3|≤1 .

    (1)若且为真，求实数的取值范围；

    (2)若是的充分不必要条件,求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)，当x，y∈R时，恒有f(x＋y)＝f(x)＋f(y)．当x＞0时，f(x)＞0.

    (1)求证：f(x)是奇函数；

    (2)若f(1)＝，试求f(x)在区间[－2,6]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

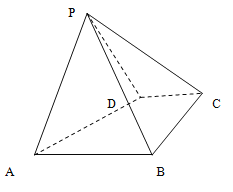
    【题目】如图，四棱锥中，底面是直角梯形，,，,侧面底面,且是以为底的等腰三角形.

    （Ⅰ）证明：

    （Ⅱ）若四棱锥的体积等于.问：是否存在过点的平面分别交，于点，使得平面平面？若存在，求出的面积；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数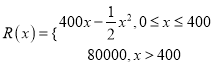： ，其中是仪器的月产量

    (1)将利润表示为月产量的函数

    （2）当月产量为何值时，公司所获利润最大？最大利润是多少元？（总收益=总成本+利润）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间；

    （2）若函数 的图象在点 处的切线的倾斜角为 ，对于任意的,函数在区间上总不是单调函数， 求的取值范围；

    （3）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列三个集合：

    ①{x|y＝x2＋1}；

    ②{y|y＝x2＋1}；

    ③{(x，y)|y＝x2＋1}．

    (1)它们是不是相同的集合？

    (2)它们各自的含义是什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业常年生产一种出口产品，根据预测可知，进入21世纪以来，该产品的产量平稳增长．记2009年为第1年，且前4年中，第x年与年产量f(x) 万件之间的关系如下表所示：

    x

    1

    2

    3

    4

    f(x)

    4.00

    5.58

    7.00

    8.44

    若f(x)近似符合以下三种函数模型之一：f(x)＝ax＋b，f(x)＝2x＋a，f(x)＝logx＋a.

    (1)找出你认为最适合的函数模型，并说明理由，然后选取其中你认为最适合的数据求出相应的解析式；

    (2)因遭受某国对该产品进行反倾销的影响，2015年的年产量比预计减少30%，试根据所建立的函数模型，确定2015年的年产量．

    查看答案和解析>>

    同步练习册答案