练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a＞l，函数y＝|logax|的定义域为[m，n](m＜n)，值域为[0，1]．定义“区间[m，n]的长度等于n－m”，若区间[m，n]长度的最小值为，则实数a的值为

    [　　]

    A．11

    B．6

    C．

    D．

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黄冈市黄梅一中2009届高三数学试题5(理科) 题型：044

    已知点P在曲线C：y＝(x＞1)上，设曲线C在点P处的切线为l，若l与函数y＝kx(k＞0)的图像交于点A，与X轴相交于B点，设点P的横坐标为t，设A，B的横坐标分别为xA，xB，记f(t)＝xA·xB

    (1)求函数f(t)的解析式

    (2)设数列{an}(n≥1，n∈N)满足a1＝1，an＝f()(n≥2)，设数列{bn}(n≥1，n∈N，满足bn＝－，求{an}和{bn}的通项公式

    (3)在(2)的条件下，当1＜k＜3时，证明不等式a1＋a2＋a3…＋an＞．

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省、兰溪一中高二下期中理科数学试卷（解析版） 题型：解答题

    （1）已知函数f(x)=x－ax+(a－1)，。讨论函数的单调性；       

    （2）.已知函数f (x)=lnx，g(x)=ex．设直线l为函数 y＝f (x) 的图象上一点A(x0，f (x0))处的切线．问在区间(1，+∞)上是否存在x0，使得直线l与曲线y=g(x)也相切．若存在，这样的x0有几个？，若没有，则说明理由。

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省高三下学期2月月考理科数学试卷 题型：解答题

    （本题满分14分）已知函数f (x)=lnx，g(x)=ex．

     （I）若函数φ (x) = f (x)－，求函数φ (x)的单调区间；

     （Ⅱ）设直线l为函数 y＝f (x) 的图象上一点A(x0，f (x0))处的切线．证明：在区间(1，+∞)上存在唯一的x0，使得直线l与曲线y=g(x)相切．

    注：e为自然对数的底数．

     

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州十四中2011-2012学年高三2月月考试题-数学（理） 题型：解答题

     

        已知函数f （x）=lnx，g（x）=ex．

        （I）若函数φ （x） = f （x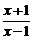）－，求函数φ （x）的单调区间；

        （Ⅱ）设直线l为函数 y＝f （x） 的图象上一点A（x0，f （x0））处的切线．证明：在区间（1，+∞）上存在唯一的x0，使得直线l与曲线y=g（x）相切．

        注：e为自然对数的底数．

     

     

     

    查看答案和解析>>

    同步练习册答案