
分析 依题意,知2an+1-an=n,2an-an-1=n-1(n≥2),两式相减可得2(an+1-an-1)=an-an-1-1(n≥2),令bn=an+1-an-1,易证数列{bn}是公比为$\frac{1}{2}$等比数列,易求b1=a2-a1-1=-$\frac{3}{4}$,从而可求得bn,再利用等比数列的求和公式及累加法可求得an;最后利用分组求和法可得Sn.
解答 解:∵点(n,2an+1-an)(n∈N+)在直线y=x上,
∴2an+1-an=n,
∴2an-an-1=n-1(n≥2),
两式相减得:2(an+1-an)-(an-an-1)=1(n≥2),
即2(an+1-an-1)=an-an-1-1(n≥2),
又bn=an+1-an-1,
∴bn=$\frac{1}{2}$bn-1(n≥2),
∴数列{bn}是公比为$\frac{1}{2}$等比数列,又a1=$\frac{1}{2}$,2a2-a1=1,故a2=$\frac{3}{4}$,所以b1=a2-a1-1=-$\frac{3}{4}$,
∴bn=(-$\frac{3}{4}$)×$(\frac{1}{2})^{{n}^{-1}}$;
∴b1+b2+…+bn-1=[(a2-a1-1)+(a3-a2-1)+…+(an-an-1-1)]=an-a1-(n-1)=$\frac{-\frac{3}{4}(1-{(\frac{1}{2})}^{n-1})}{1-\frac{1}{2}}$=-$\frac{3}{2}$+3×$(\frac{1}{2})^{n}$,
∴an=(n-2)+3×$(\frac{1}{2})^{n}$,
∴Sn=a1+a2+…+an=[(-1+0+1+…+(n-2)]+3[$\frac{1}{2}$+$(\frac{1}{2})^{2}$+…+${(\frac{1}{2})}^{n}$]=$\frac{(n-3)n}{2}$+3×$\frac{\frac{1}{2}(1-{(\frac{1}{2})}^{n})}{1-\frac{1}{2}}$=$\frac{{n}^{2}-3n+6}{2}$-3×$(\frac{1}{2})^{n}$.
点评 本题考查递推数列的关系式的应用,考查等比关系的确定是关键,突出考查累加法与分组求和,考查等价转化思想与综合运算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标系 中,动点
中,动点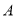 的坐标为
的坐标为 ,其中
,其中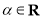 .在极坐标系(以原点
.在极坐标系(以原点 为极点,以
为极点,以 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线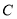 的方程为
的方程为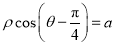 .
.
(Ⅰ)判断动点 的轨迹的形状;
的轨迹的形状;
(Ⅱ)若直线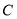 与动点
与动点 的轨迹有且仅有一个公共点,求实数
的轨迹有且仅有一个公共点,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com