
дкЦНУцжБНЧзјБъЯЕxOyжа,FЪЧХзЮяЯпC:x2=2py(p>0)ЕФНЙЕу,MЪЧХзЮяЯпCЩЯЮЛгкЕквЛЯѓЯоФкЕФШЮвтвЛЕу,Й§M,F,OШ§ЕуЕФдВЕФдВаФЮЊQ,ЕуQЕНХзЮяЯпCЕФзМЯпЕФОрРыЮЊ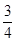 .
.
(1)ЧѓХзЮяЯпCЕФЗНГЬ;
(2)ЪЧЗёДцдкЕуM,ЪЙЕУжБЯпMQгыХзЮяЯпCЯрЧагкЕуM?ШєДцдк,ЧѓГіЕуMЕФзјБъ;ШєВЛДцдк,ЫЕУїРэгЩ.
(3)ШєЕуMЕФКсзјБъЮЊ ,жБЯпl:y=kx+
,жБЯпl:y=kx+ гыХзЮяЯпCгаСНИіВЛЭЌЕФНЛЕуA,B,lгыдВQгаСНИіВЛЭЌЕФНЛЕуD,E,ЧѓЕБ
гыХзЮяЯпCгаСНИіВЛЭЌЕФНЛЕуA,B,lгыдВQгаСНИіВЛЭЌЕФНЛЕуD,E,ЧѓЕБ ЁмkЁм2ЪБ,|AB|2+|DE|2ЕФзюаЁжЕ.
ЁмkЁм2ЪБ,|AB|2+|DE|2ЕФзюаЁжЕ.
ЃЈ1ЃЉx2=2y ЃЈ2ЃЉДцдкЕуM( ,1) ЃЈ3ЃЉ
,1) ЃЈ3ЃЉ
НтЮіНт:(1)вРЬтвтжЊF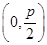 ,дВаФQдкЯпЖЮOFЕФДЙжБЦНЗжЯпy=
,дВаФQдкЯпЖЮOFЕФДЙжБЦНЗжЯпy= ЩЯ,
ЩЯ,
вђЮЊХзЮяЯпCЕФзМЯпЗНГЬЮЊy=-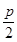 ,
,
Ыљвд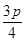 =
=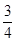 ,
,
МДp=1.
вђДЫХзЮяЯпCЕФЗНГЬЮЊx2=2y.
(2)МйЩшДцдкЕуM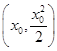 (x0>0)ТњзуЬѕМў,ХзЮяЯпCдкЕуMДІЕФЧаЯпаБТЪЮЊyЁф
(x0>0)ТњзуЬѕМў,ХзЮяЯпCдкЕуMДІЕФЧаЯпаБТЪЮЊyЁф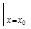 =
=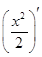
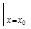 =x0,
=x0,
ЫљвджБЯпMQЕФЗНГЬЮЊy-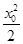 =x0(x-x0).
=x0(x-x0).
Сюy= ЕУxQ=
ЕУxQ= +
+ .
.
ЫљвдQЃЈ +
+ ,
, ЃЉ.
ЃЉ.
гж|QM|=|OQ|,
ЙЪЃЈ -
- ЃЉ2+ЃЈ
ЃЉ2+ЃЈ -
-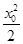 ЃЉ2=ЃЈ
ЃЉ2=ЃЈ +
+ ЃЉ2+
ЃЉ2+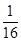 ,
,
вђДЫЃЈ -
-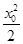 ЃЉ2=
ЃЉ2=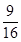 .
.
гжx0>0,
Ыљвдx0= ,ДЫЪБM(
,ДЫЪБM( ,1).
,1).
ЙЪДцдкЕуM( ,1),
,1),
ЪЙЕУжБЯпMQгыХзЮяЯпCЯрЧагкЕуM.
(3)ЕБx0= ЪБ,гЩ(2)ЕУQЃЈ
ЪБ,гЩ(2)ЕУQЃЈ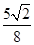 ,
, ЃЉ,
ЃЉ,
ЈQЕФАыОЖЮЊr=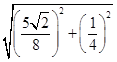 =
= ,
,
ЫљвдЈQЕФЗНГЬЮЊЃЈx-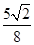 ЃЉ2+ЃЈy-
ЃЉ2+ЃЈy- ЃЉ2=
ЃЉ2=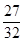 .
.
гЩ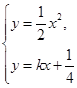
ећРэЕУ2x2-4kx-1=0.
ЩшA,BСНЕуЕФзјБъЗжБ№ЮЊ(x1,y1),(x2,y2),
гЩгкІЄ1=16k2+8>0,x1+x2=2k,x1x2=- ,
,
Ыљвд|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)(4k2+2).
гЩ
ећРэЕУ(1+k2)x2-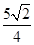 x-
x-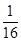 =0.
=0.
ЩшD,EСНЕуЕФзјБъЗжБ№ЮЊ(x3,y3),(x4,y4),
гЩгкІЄ2=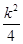 +
+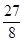 >0,x3+x4=
>0,x3+x4=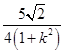 ,
,
x3x4=- .
.
Ыљвд|DE|2=(1+k2)[(x3+x4)2-4x3x4]
= +
+ .
.
вђДЫ|AB|2+|DE|2=(1+k2)(4k2+2)+  +
+ .
.
Сю1+k2=t,
гЩгк ЁмkЁм2,
ЁмkЁм2,
дђ ЁмtЁм5,
ЁмtЁм5,
Ыљвд|AB|2+|DE|2=t(4t-2)+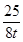 +
+
=4t2-2t+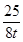 +
+

 аЁбЇПЮЬУзївЕЯЕСаД№АИ
аЁбЇПЮЬУзївЕЯЕСаД№АИ Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊЫЋЧњЯпЙ§Еу(3ЃЌЃ2)ЃЌЧвгыЭждВ4x2ЃЋ9y2ЃН36гаЯрЭЌЕФНЙЕуЃЎ
(1)ЧѓЫЋЧњЯпЕФБъзМЗНГЬЃЛ
(2)ЧѓвдЫЋЧњЯпЕФгвзМЯпЮЊзМЯпЕФХзЮяЯпЕФБъзМЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
Й§ЫЋЧњЯп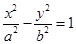
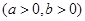 ЕФзѓНЙЕу
ЕФзѓНЙЕу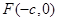
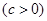 ЃЌзїЧуаБНЧЮЊ
ЃЌзїЧуаБНЧЮЊ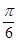 ЕФжБЯп
ЕФжБЯп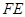 НЛИУЫЋЧњЯпгвжЇгкЕу
НЛИУЫЋЧњЯпгвжЇгкЕу ЃЌШє
ЃЌШє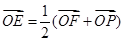 ЃЌЧв
ЃЌЧв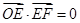 ЃЌдђЫЋЧњЯпЕФРыаФТЪЮЊ__________ЃЎ
ЃЌдђЫЋЧњЯпЕФРыаФТЪЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ШчЭМ,ЭждВЕФжааФЮЊдЕуO,ГЄжсдкxжсЩЯ,РыаФТЪe= ,Й§зѓНЙЕуF1зїxжсЕФДЙЯпНЛЭждВгкAЁЂAЁфСНЕу,
,Й§зѓНЙЕуF1зїxжсЕФДЙЯпНЛЭждВгкAЁЂAЁфСНЕу,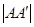 =4.
=4.
(1)ЧѓИУЭждВЕФБъзМЗНГЬ;
(2)ШЁЦНаагкyжсЕФжБЯпгыЭждВЯрНЛгкВЛЭЌЕФСНЕуPЁЂPЁф,Й§PЁЂPЁфзїдВаФЮЊQЕФдВ,ЪЙЭждВЩЯЕФЦфгрЕуОљдкдВQЭт.ЧѓЁїPPЁфQЕФУцЛ§SЕФзюДѓжЕ,ВЂаДГіЖдгІЕФдВQЕФБъзМЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ШчЭМЫљЪО,ЩшЭждВЕФжааФЮЊдЕуO,ГЄжсдкxжсЩЯ,ЩЯЖЅЕуЮЊA,зѓЁЂгвНЙЕуЗжБ№ЮЊF1ЁЂF2,ЯпЖЮOF1ЁЂOF2ЕФжаЕуЗжБ№ЮЊB1ЁЂB2,ЧвЁїAB1B2ЪЧУцЛ§ЮЊ4ЕФжБНЧШ§НЧаЮ.
(1)ЧѓИУЭждВЕФРыаФТЪКЭБъзМЗНГЬ;
(2)Й§B1зїжБЯпНЛЭждВгкPЁЂQСНЕу,ЪЙPB2ЁЭQB2,ЧѓЁїPB2QЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊЫЋЧњЯпCЕФЗНГЬЮЊ -
- =1(a>0,b>0),РыаФТЪe=
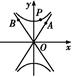
=1(a>0,b>0),РыаФТЪe= ,ЖЅЕуЕННЅНќЯпЕФОрРыЮЊ
,ЖЅЕуЕННЅНќЯпЕФОрРыЮЊ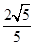 .
.
(1)ЧѓЫЋЧњЯпCЕФЗНГЬ;
(2)ШчЭМ,PЪЧЫЋЧњЯпCЩЯвЛЕу,AЁЂBСНЕудкЫЋЧњЯпCЕФСНЬѕНЅНќЯпЩЯ,ЧвЗжБ№ЮЛгкЕквЛЁЂЖўЯѓЯо.Шє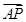 =ІЫ
=ІЫ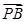 ,ІЫЁЪ
,ІЫЁЪ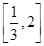 .ЧѓЁїAOBЕФУцЛ§ЕФШЁжЕЗЖЮЇ.
.ЧѓЁїAOBЕФУцЛ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ЩшЭждВ +
+ =1(a>b>0)ЕФзѓ,гвНЙЕуЗжБ№ЮЊF1,F2,ЕуP(a,b)Тњзу|PF2|=|F1F2|.
=1(a>b>0)ЕФзѓ,гвНЙЕуЗжБ№ЮЊF1,F2,ЕуP(a,b)Тњзу|PF2|=|F1F2|.
(1)ЧѓЭждВЕФРыаФТЪe;
(2)ЩшжБЯпPF2гыЭждВЯрНЛгкA,BСНЕу.ШєжБЯпPF2гыдВ(x+1)2+(y- )2=16ЯрНЛгкM,NСНЕу,Чв|MN|=
)2=16ЯрНЛгкM,NСНЕу,Чв|MN|= |AB|,ЧѓЭждВЕФЗНГЬ.
|AB|,ЧѓЭждВЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
Й§ЭждВ ЕФзѓЖЅЕу
ЕФзѓЖЅЕу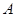 зїаБТЪЮЊ2ЕФжБЯпЃЌгыЭждВЕФСэвЛИіНЛЕуЮЊ
зїаБТЪЮЊ2ЕФжБЯпЃЌгыЭждВЕФСэвЛИіНЛЕуЮЊ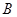 ЃЌгы
ЃЌгы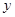 жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ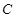 ЃЌвбжЊ
ЃЌвбжЊ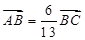 .
.
ЃЈ1ЃЉЧѓЭждВЕФРыаФТЪЃЛ
ЃЈ2ЃЉЩшЖЏжБЯп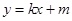 гыЭждВгаЧвжЛгавЛИіЙЋЙВЕу
гыЭждВгаЧвжЛгавЛИіЙЋЙВЕу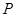 ЃЌЧвгыжБЯп
ЃЌЧвгыжБЯп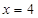 ЯрНЛгкЕу
ЯрНЛгкЕу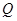 ЃЌШє
ЃЌШє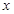 жсЩЯДцдквЛЖЈЕу
жсЩЯДцдквЛЖЈЕу ЃЌЪЙЕУ
ЃЌЪЙЕУ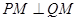 ЃЌЧѓЭждВЕФЗНГЬ.
ЃЌЧѓЭждВЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊЭждВC: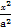 +
+ =1(a>b>0)ЕФгвНЙЕуЮЊF(1,0),ЧвЕу(-1,
=1(a>b>0)ЕФгвНЙЕуЮЊF(1,0),ЧвЕу(-1,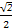 )дкЭждВCЩЯ.
)дкЭждВCЩЯ.
(1)ЧѓЭждВCЕФБъзМЗНГЬ.
(2)вбжЊЕуQ( ,0),ЖЏжБЯпlЙ§ЕуF,ЧвжБЯпlгыЭждВCНЛгкA,BСНЕу,жЄУї:
,0),ЖЏжБЯпlЙ§ЕуF,ЧвжБЯпlгыЭждВCНЛгкA,BСНЕу,жЄУї: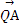 ЁЄ
ЁЄ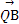 ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com