
某糖果公司的一条流水线不论生产与否每天都要支付3000元的固定费用(管理费、房租、还贷款、维修等),它生产1千克糖果的成本为10元,而销售价是1千克15元,试问:每天应当生产并售出多少千克糖果,才能使收支平衡,即它的盈亏平衡点是多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 3a | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 2 |
| x |
| 2(a-x) |
查看答案和解析>>
科目:高中数学 来源:2011届福建省莆田市高中高三毕业班适应性练习理科数学 题型:解答题
(本小题满分13分)
某公司有价值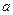 万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值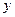 万元与技术改造投入
万元与技术改造投入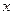 万元之间的关系满足:①
万元之间的关系满足:①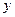 与
与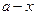 和
和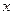 的乘积成正比;②
的乘积成正比;②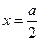 时,
时,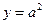 ;③
;③ ,其中
,其中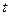 为常数,且
为常数,且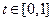 .
.
(Ⅰ)设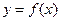 ,求
,求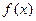 表达式,并求
表达式,并求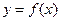 的定义域;
的定义域;
(Ⅱ)求 出附加值
出附加值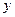 的最大值,并求出此时的技术改造投入.
的最大值,并求出此时的技术改造投入.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省莆田市高三毕业班适应性练习理科数学 题型:解答题
(本小题满分13分)
某公司有价值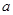 万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值 万元与技术改造投入
万元与技术改造投入 万元之间的关系满足:①
万元之间的关系满足:① 与
与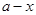 和
和 的乘积成正比;②
的乘积成正比;② 时,
时,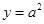 ;③
;③ ,其中
,其中 为常数,且
为常数,且 .
.
(Ⅰ)设 ,求
,求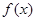 表达式,并求
表达式,并求 的定义域;
的定义域;
(Ⅱ)求出附加值 的最大值,并求出此时的技术改造投入.
的最大值,并求出此时的技术改造投入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com