
ЎѕМвДїЎї2016Дк6ФВ22ИХЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±ФЪЙЅ¶«ЗаµєїЄД».ОЄБЛЅвДДР©ИЛёь№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±Ј¬Ді»ъ№№Лж»ъійИЎБЛДкБдФЪ15ЎЄ75ЛкЦ®јдµД100ИЛЅшРРµчІйЈ¬Іў°ґДкБд»жЦЖіЙЖµВК·ЦІјЦ±·ЅНјЈ¬ИзНјЛщКѕЈ¬Жд·ЦЧйЗшјдОЄЈє ![]() .°СДкБдВдФЪЗшјдЧФ
.°СДкБдВдФЪЗшјдЧФ![]() єН
єН![]() ДЪµДИЛ·Ц±ріЖОЄЎ°ЗаЙЩДкЎ±єНЎ°ЦРАПДкЎ±.
ДЪµДИЛ·Ц±ріЖОЄЎ°ЗаЙЩДкЎ±єНЎ°ЦРАПДкЎ±.

№ШЧў | І»№ШЧў | єПјЖ | |
ЗаЙЩДк | 15 | ||
ЦРАПДк | |||
єПјЖ | 50 | 50 | 100 |
ЈЁ1Ј©ёщѕЭЖµВК·ЦІјЦ±·ЅНјЗуСщ±ѕµДЦРО»КэЈЁ±ЈБфБЅО»РЎКэ)єНЦЪКэЈ»
ЈЁ2Ј©ёщѕЭТСЦЄМхјюНкіЙПВГжµД![]() БРБЄ±нЈ¬ІўЕР¶ПДЬ·сУР
БРБЄ±нЈ¬ІўЕР¶ПДЬ·сУР![]() µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±Ј»
µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±Ј»
БЩЅзЦµ±нЈє
ёЅЈєІОїј№«КЅ
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
 Ј¬ЖдЦР
Ј¬ЖдЦР![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©36.43Ј»ЈЁ2Ј©УР![]() µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±КФМв
µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±КФМв
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁўсЈ©ёщѕЭЖµВК·ЦІјЦ±·ЅНјЦРЦЪКэКЗЧоёЯРЎѕШРОµЧ±ЯµДЦРµгЈ¬ЗуіцјґїЙЈ»АыУГЦРО»КэБЅ±ЯЖµВКПаµИЈ¬БР·ЅіМЗуіцЦРО»КэµДЦµЈ»
ЈЁўтЈ©ТАМвТвНкіЙ2ЎБ2БРБЄ±нЈ¬јЖЛгK2Ј¬¶ФХХБЩЅзЦµµГіцЅбВЫЈ®
КФМвЅвОцЈє
ЈЁ1Ј©ёщѕЭЖµВК·ЦІјЦ±·ЅНјїЙЦЄСщ±ѕµДЦЪКэОЄ40Ј¬ТтОЄ![]() Ј¬
Ј¬
ЙиСщ±ѕµДЦРО»КэОЄ![]() Ј¬Фт
Ј¬Фт![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬јґСщ±ѕµДЦРО»КэФјОЄ36.43.
Ј¬јґСщ±ѕµДЦРО»КэФјОЄ36.43.
ЈЁ2Ј©ТАМвТвїЙєНЈ¬ійИЎµДЎ°ЗаЙЩДкЎ±№ІУР![]() ИЛЈ¬Ў°ЦРАПДкЎ±№ІУР
ИЛЈ¬Ў°ЦРАПДкЎ±№ІУР![]() ИЛ.
ИЛ.
НкіЙµД![]() БРБЄ±нИзПВЈє
БРБЄ±нИзПВЈє
№ШЧў | І»№ШЧў | єПјЖ | |
ЗаЙЩДк | 15 | 30 | 45 |
ЦРАПДк | 35 | 20 | 55 |
єПјЖ | 50 | 50 | 100 |
ЅбєПБРБЄ±нµДКэѕЭµГ Ј¬ТтОЄ
Ј¬ТтОЄ![]() Ј¬
Ј¬
ЛщТФУР![]() µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±.
µД°СОХИПОЄЎ°ЦРАПДкЎ±±ИЎ°ЗаЙЩДкЎ±ёьјУ№ШЧўЎ°№ъјКЅМУэРЕПў»Їґу»бЎ±.


 їЪЛгМвїЁјУУ¦УГМвјЇСµПµБРґр°ё
їЪЛгМвїЁјУУ¦УГМвјЇСµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄЖЅГжЛД±ЯРОABCDЈ¬AB=BC=3Ј¬CD=1Ј¬AD= ![]() Ј¬ЎПADC=90ЎгЈ¬СШЦ±ПЯACЅ«ЎчACD·ХЫіЙЎчACDЎдЈ¬Ц±ПЯACУлBDЎдЛщіЙЅЗµДУаПТµДЧоґуЦµКЗ Ј®
Ј¬ЎПADC=90ЎгЈ¬СШЦ±ПЯACЅ«ЎчACD·ХЫіЙЎчACDЎдЈ¬Ц±ПЯACУлBDЎдЛщіЙЅЗµДУаПТµДЧоґуЦµКЗ Ј® 
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиєЇКэfЈЁxЈ©=|x+4|Ј®
ЈЁ1Ј©Ифy=fЈЁ2x+aЈ©+fЈЁ2x©ЃaЈ©ЧоРЎЦµОЄ4Ј¬ЗуaµДЦµЈ»
ЈЁ2Ј©ЗуІ»µИКЅfЈЁxЈ©Јѕ1©Ѓ ![]() xµДЅвјЇЈ®
xµДЅвјЇЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЛщКѕКЗєЇКэ![]() ФЪЗшјд
ФЪЗшјд![]() ЙПµДНјПуЈ¬ОЄБЛµГµЅХвёцєЇКэµДНјПсЈ¬Ц»ТЄЅ«
ЙПµДНјПуЈ¬ОЄБЛµГµЅХвёцєЇКэµДНјПсЈ¬Ц»ТЄЅ«![]() µДНјПуЙПЛщУРµДµг ( )
µДНјПуЙПЛщУРµДµг ( )

A. ПтЧуЖЅТЖ![]() ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЛх¶МµЅФАґµД
ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЛх¶МµЅФАґµД![]() ±¶Ј¬ЧЭЧш±кІ»±д
±¶Ј¬ЧЭЧш±кІ»±д
B. ПтЧуЖЅТЖ![]() ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЙмі¤µЅФАґµД2±¶Ј¬ЧЭЧш±кІ»±д
ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЙмі¤µЅФАґµД2±¶Ј¬ЧЭЧш±кІ»±д
C. ПтЧуЖЅТЖ![]() ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЙмі¤µЅФАґµД2±¶Ј¬ЧЭЧш±кІ»±д
ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЙмі¤µЅФАґµД2±¶Ј¬ЧЭЧш±кІ»±д
D. ПтЧуЖЅТЖ![]() ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЛх¶МµЅФАґµД
ёцµҐО»і¤¶ИЈ¬ФЩ°СЛщµГёчµгµДєбЧш±кЛх¶МµЅФАґµД![]() ±¶Ј¬ЧЭЧш±кІ»±д
±¶Ј¬ЧЭЧш±кІ»±д
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэf(x)=|x©Ѓa|Ј¬gЈЁxЈ©=x2+2ax+1ЈЁaОЄХэКµКэЈ©Ј¬ВъЧгf(0)=g(0)Ј»
єЇКэF(x)=f(x)+g(x)+b¶ЁТеУтОЄDЈ®
ЈЁ1Ј©ЗуaµДЦµЈ»
ЈЁ2Ј©ИфґжФЪx0ЎКDЈ¬К№F(x0)=x0іЙБўЈ¬ЗуКµКэbµДИЎЦµ·¶О§Ј»
ЈЁ3Ј©ИфnОЄХэХыКэЈ¬Ц¤ГчЈє![]() Јј4Ј®
Јј4Ј®
ЈЁІОїјКэѕЭЈєlg3=0.3010Ј¬ ![]() =0.1342Ј¬
=0.1342Ј¬![]() =0.0281Ј¬
=0.0281Ј¬![]() =0.0038Ј©
=0.0038Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЅ№ѕаОЄ2µДНЦФІWЈє ![]() =1ЈЁaЈѕbЈѕ0Ј©µДЧуЎўУТЅ№µг·Ц±рОЄA1 Ј¬ A2 Ј¬ ЙПЎўПВ¶Ґµг·Ц±рОЄB1 Ј¬ B2 Ј¬ µгMЈЁx0 Ј¬ y0Ј©ОЄНЦФІWЙПІ»ФЪЧш±кЦбЙПµДИОТвТ»µгЈ¬ЗТЛДМхЦ±ПЯMA1 Ј¬ MA2 Ј¬ MB1 Ј¬ MB2µДР±ВКЦ®»эОЄ
=1ЈЁaЈѕbЈѕ0Ј©µДЧуЎўУТЅ№µг·Ц±рОЄA1 Ј¬ A2 Ј¬ ЙПЎўПВ¶Ґµг·Ц±рОЄB1 Ј¬ B2 Ј¬ µгMЈЁx0 Ј¬ y0Ј©ОЄНЦФІWЙПІ»ФЪЧш±кЦбЙПµДИОТвТ»µгЈ¬ЗТЛДМхЦ±ПЯMA1 Ј¬ MA2 Ј¬ MB1 Ј¬ MB2µДР±ВКЦ®»эОЄ ![]() Ј®
Ј®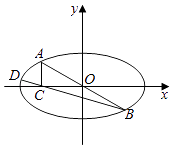
ЈЁ1Ј©ЗуНЦФІWµД±кЧј·ЅіМЈ»
ЈЁ2Ј©ИзНјЛщКѕЈ¬µгAЈ¬DКЗНЦФІWЙПБЅµгЈ¬µгAУлµгB№ШУЪФµг¶ФіЖЈ¬ADЎНABЈ¬µгCФЪxЦбЙПЈ¬ЗТACУлxЦбґ№Ц±Ј¬ЗуЦ¤ЈєBЈ¬CЈ¬DИэµг№ІПЯЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиР±ВКОЄ2µДЦ±ПЯlЈ¬№эЛ«ЗъПЯ![]() µДУТЅ№ µгЈ¬ЗТУлЛ«ЗъПЯµДЧуЎўУТБЅЦ§·Ц±рПаЅ»Ј¬ФтЛ«ЗъПЯАлРДВКЈ¬eµДИЎЦµ·¶О§КЗ ЈЁ Ј©
µДУТЅ№ µгЈ¬ЗТУлЛ«ЗъПЯµДЧуЎўУТБЅЦ§·Ц±рПаЅ»Ј¬ФтЛ«ЗъПЯАлРДВКЈ¬eµДИЎЦµ·¶О§КЗ ЈЁ Ј©
A. eЈѕ![]() B. eЈѕ
B. eЈѕ![]() C. 1ЈјeЈј
C. 1ЈјeЈј![]() D. 1ЈјeЈј
D. 1ЈјeЈј![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ТСЦЄНЦФІ
ЦРЈ¬ТСЦЄНЦФІ![]() Јє
Јє ![]() µДАлРДВК
µДАлРДВК![]() Ј¬Ч󶥵гОЄ
Ј¬Ч󶥵гОЄ![]() Ј¬№эµг
Ј¬№эµг![]() ЧчР±ВКОЄ
ЧчР±ВКОЄ![]() µДЦ±ПЯ
µДЦ±ПЯ![]() Ѕ»НЦФІ
Ѕ»НЦФІ![]() УЪµг
УЪµг![]() Ј¬Ѕ»
Ј¬Ѕ»![]() ЦбУЪµг
ЦбУЪµг![]() Ј®
Ј®

ЈЁ1Ј©ЗуНЦФІ![]() µД·ЅіМЈ»
µД·ЅіМЈ»
ЈЁ2Ј©ТСЦЄ![]() ОЄ
ОЄ![]() µДЦРµгЈ¬КЗ·сґжФЪ¶Ёµг
µДЦРµгЈ¬КЗ·сґжФЪ¶Ёµг![]() Ј¬¶ФУЪИОТвµД
Ј¬¶ФУЪИОТвµД![]() ¶јУР
¶јУР![]() Ј¬ИфґжФЪЈ¬Зуіцµг
Ј¬ИфґжФЪЈ¬Зуіцµг![]() µД
µД
Чш±кЈ»ИфІ»ґжФЪЛµГчАнУЙЈ»
ЈЁ3Ј©Иф№э![]() µгЧчЦ±ПЯ
µгЧчЦ±ПЯ![]() µДЖЅРРПЯЅ»НЦФІ
µДЖЅРРПЯЅ»НЦФІ![]() УЪµг
УЪµг![]() Ј¬Зу
Ј¬Зу![]() µДЧоРЎЦµЈ®
µДЧоРЎЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛЅвґєјѕЦзТ№ОВІоґуРЎУлДіЦЦЧУ·ўСї¶аЙЩЦ®јдµД№ШПµЈ¬ПЦФЪґУ![]() ФВ·ЭµД
ФВ·ЭµД![]() МмЦРЛж»ъМфСЎБЛ
МмЦРЛж»ъМфСЎБЛ![]() МмЅшРРСРѕїЈ¬ЗТ·Ц±рјЗВјБЛГїМмЦзТ№ОВІоУлГїМм
МмЅшРРСРѕїЈ¬ЗТ·Ц±рјЗВјБЛГїМмЦзТ№ОВІоУлГїМм![]() їЕЦЦЧУЅюЕЭєуµД·ўСїКэЈ¬µГµЅИзПВ±нёсЈє
їЕЦЦЧУЅюЕЭєуµД·ўСїКэЈ¬µГµЅИзПВ±нёсЈє
ИХЖЪ |
|
|
|
|
|
ОВІо |
|
|
|
|
|
·ўСїКэ |
|
|
|
|
|
ЈЁ![]() Ј©ґУХв
Ј©ґУХв![]() МмЦРИОСЎ
МмЦРИОСЎ![]() МмЈ¬јЗ·ўСїµДЦЦЧУКэ·Ц±рОЄ
МмЈ¬јЗ·ўСїµДЦЦЧУКэ·Ц±рОЄ![]() Ј¬
Ј¬ ![]() Ј¬ЗуКВјюЎ°
Ј¬ЗуКВјюЎ°![]() Ј¬
Ј¬ ![]() ѕщІ»РЎУЪ
ѕщІ»РЎУЪ![]() Ў±µДёЕВКЈ®
Ў±µДёЕВКЈ®
ЈЁ![]() Ј©ґУХв
Ј©ґУХв![]() МмЦРИОСЎ
МмЦРИОСЎ![]() МмЈ¬ИфСЎИЎµДКЗ
МмЈ¬ИфСЎИЎµДКЗ![]() ФВ
ФВ![]() ИХУл
ИХУл![]() ФВ
ФВ![]() ИХµДБЅЧйКэѕЭЈ¬ЗлёщѕЭХв
ИХµДБЅЧйКэѕЭЈ¬ЗлёщѕЭХв![]() МмЦРµДБн
МмЦРµДБн![]() МмµДКэѕЭЈ¬Зуіц
МмµДКэѕЭЈ¬Зуіц![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() Ј®
Ј®
ЈЁ![]() Ј©ИфУЙПЯРФ»Ш№й·ЅіМµГµЅµД№АјЖКэѕЭУлЛщСЎіцµДБЅЧйјмСйКэѕЭµДОуІоѕщІ»і¬№э
Ј©ИфУЙПЯРФ»Ш№й·ЅіМµГµЅµД№АјЖКэѕЭУлЛщСЎіцµДБЅЧйјмСйКэѕЭµДОуІоѕщІ»і¬№э![]() їЕЈ¬ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµДЈ¬КФОКЈЁ
їЕЈ¬ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµДЈ¬КФОКЈЁ![]() Ј©ЦРЛщµГµДПЯРФ»Ш№й·ЅіМКЗ·сїЙїїЈї
Ј©ЦРЛщµГµДПЯРФ»Ш№й·ЅіМКЗ·сїЙїїЈї
ЈЁІОїј№«КЅЈє  Ј®
Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com