
【题目】以下关于圆锥曲线的命题中:
①双曲线![]() 与椭圆
与椭圆![]() 有相同焦点;
有相同焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设![]() 、
、![]() 为两个定点,
为两个定点,![]() 为常数,若
为常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线;
的轨迹为双曲线;
④过抛物线![]() 的焦点作直线与抛物线相交于
的焦点作直线与抛物线相交于![]() 、
、![]() ,则使它们的横坐标之和等于5的直线有且只有两条;
,则使它们的横坐标之和等于5的直线有且只有两条;
以上命题正确的个数为( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是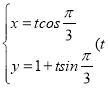 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,射线
两点,射线![]() 与直线
与直线![]() 交于
交于![]() 点,若
点,若![]() 的面积为1,求
的面积为1,求![]() 的值和弦长
的值和弦长![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
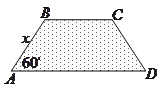
【题目】扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为![]() (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为![]() 平方米,且高度不低于
平方米,且高度不低于![]() 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为![]() (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段![]() 与两腰长的和)为
与两腰长的和)为![]() (米).
(米).
⑴求![]() 关于
关于![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过![]() 米,则其腰长
米,则其腰长![]() 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长![]() 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有数字1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字不大于第二张卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解初三学生的体育锻炼情况,随机抽取了40名学生对一周的体育锻炼时间长(单位:小时)进行统计,并将数据整理如下:
时间长 性别 |
|
|
|
|
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)采用样本估计总体的方式,试估计该校的所有学生中一周的体育锻炼时间长为![]() 的概率;
的概率;
(2)若将一周的体育锻炼时间长不低于3小时的评定为“体育锻炼合格者”,否则为“不合格者”,根据以上数据完成下面的![]() 列联表,并据此判断能否有95%的把握认为体育锻炼与性别有关?附:
列联表,并据此判断能否有95%的把握认为体育锻炼与性别有关?附: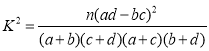 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题:其中所有正确命题的序号是_________.
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 一定是钝角三角形;
一定是钝角三角形;
③函数![]() 且
且![]() 的图象必经过点(3,2);
的图象必经过点(3,2);
④若命题“![]() ”是假命题,则实数
”是假命题,则实数![]() 的取值范围为
的取值范围为![]() ;
;
⑤![]() 的图象向左平移
的图象向左平移![]() 个单位,所得图象关于
个单位,所得图象关于![]() 轴对称.
轴对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com