
【题目】已知六面体![]() 如图所示,
如图所示,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,且满足
上的点,且满足![]() .
.
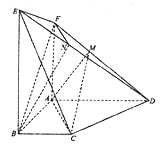
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成的二面角的大小为
所成的二面角的大小为![]() ,求
,求![]() .
.
【答案】(1)见证明;(2) ![]()
【解析】
解法一:(1)连接![]() ,设
,设![]() ,根据相似三角形以及等分线段性质,即可证明
,根据相似三角形以及等分线段性质,即可证明![]() ,连接
,连接![]() ,证明
,证明![]() 是平行四边形,得到
是平行四边形,得到![]() ,由两平面平行判定定理即可得到平面
,由两平面平行判定定理即可得到平面![]() 平面
平面![]() 。
。
解法二:(1)由题意可得![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的法向量,分别与平面
的法向量,分别与平面![]() 中两个相交向量相乘等于0,即可证明平面
中两个相交向量相乘等于0,即可证明平面![]()
![]() 平面
平面![]() ;
;
(2)由(1)可得平面![]() 的法向量,再求出平面
的法向量,再求出平面![]() 的法向量,进而求得平面
的法向量,进而求得平面![]() 与平面
与平面![]() 所成的二面角的余弦值,由此求出
所成的二面角的余弦值,由此求出![]() 。
。
解:(1)证法一:连接![]() ,设
,设![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
在![]() 中,因为
中,因为![]() ,
,
所以![]() ,且
,且![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
在![]() 中,因为
中,因为![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() 是平行四边形,
是平行四边形,
所以![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
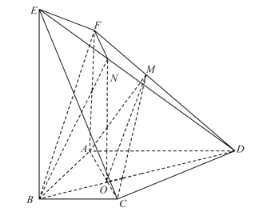
证法二:因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
取![]() 所在直线为
所在直线为![]() 轴,取
轴,取![]() 所在直线为
所在直线为![]() 轴,取
轴,取![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
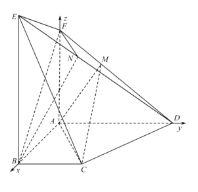
由已知可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,因为
,因为![]() ,
,
所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
同理可求![]() 点的坐标为
点的坐标为![]() ,
,
所以![]() ,
,![]() ,设
,设![]() 为平面
为平面![]() 的法向量,
的法向量,
则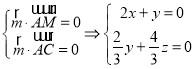 ,令
,令![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,
,
所以平面![]() 平面
平面![]()
(2)![]() 为平面
为平面![]() 的法向量.
的法向量.
![]() ,
,![]()
可求平面![]() 的一个法向量为
的一个法向量为![]()
所以![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中:
①双曲线![]() 与椭圆
与椭圆![]() 有相同焦点;
有相同焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设![]() 、
、![]() 为两个定点,
为两个定点,![]() 为常数,若
为常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线;
的轨迹为双曲线;
④过抛物线![]() 的焦点作直线与抛物线相交于
的焦点作直线与抛物线相交于![]() 、
、![]() ,则使它们的横坐标之和等于5的直线有且只有两条;
,则使它们的横坐标之和等于5的直线有且只有两条;
以上命题正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的对称轴上一点
的对称轴上一点![]() 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)记![]()
![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,是否存在
,是否存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立.若存在,求
成立.若存在,求![]() 值;若不在,说明理由.
值;若不在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com