
【题目】过抛物线![]() 的对称轴上一点
的对称轴上一点![]() 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)记![]()
![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,是否存在
,是否存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立.若存在,求
成立.若存在,求![]() 值;若不在,说明理由.
值;若不在,说明理由.
科目:高中数学 来源: 题型:
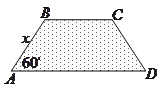
【题目】扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为![]() (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为![]() 平方米,且高度不低于
平方米,且高度不低于![]() 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为![]() (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段![]() 与两腰长的和)为
与两腰长的和)为![]() (米).
(米).
⑴求![]() 关于
关于![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过![]() 米,则其腰长
米,则其腰长![]() 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长![]() 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题:其中所有正确命题的序号是_________.
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 一定是钝角三角形;
一定是钝角三角形;
③函数![]() 且
且![]() 的图象必经过点(3,2);
的图象必经过点(3,2);
④若命题“![]() ”是假命题,则实数
”是假命题,则实数![]() 的取值范围为
的取值范围为![]() ;
;
⑤![]() 的图象向左平移
的图象向左平移![]() 个单位,所得图象关于
个单位,所得图象关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一环保型企业,为了节约成本拟进行生产改造,现将某种产品产量![]() 与单位成本
与单位成本![]() 统计数据如下:
统计数据如下:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
产量(千件) | 2 | 3 | 4 | 5 | 4 | 5 |
单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
(Ⅰ)试确定回归方程![]() ;
;
(Ⅱ)指出产量每增加1000件时,单位成本平均下降多少?
(Ⅲ)假定单位成本为70元/件时,产量应为多少件?
(参考公式: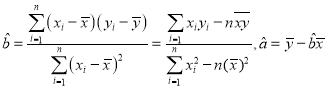 .)
.)
(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;

(2)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
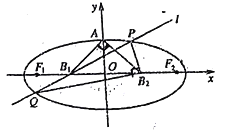
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左右焦点分别为
,左右焦点分别为![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形,过
是面积为4的直角三角形,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,则直线
,则直线![]() 的斜率为______.
的斜率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=9上的动点P在x轴、y轴上的射影分别是P1,P2,点M满足![]() .
.
(1)求点M的轨迹C的方程;
(2)点A(0,1),B(0,﹣3),过点B的直线与轨迹C交于点S,N,且直线AS、AN的斜率kAS,kAN存在,求证:kASkAN为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+y-6=0,过直线上一点P作圆x2+y2=4的切线,切点分别为A,B,则四边形PAOB面积的最小值为______,此时四边形PAOB外接圆的方程为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com