
(本小题满分13分)已知函数 ,
, .
.
(Ⅰ)若 ,对于任意的
,对于任意的 ,求证:
,求证: ;
;
(Ⅱ)若函数 在其定义域内不是单调函数,求实数
在其定义域内不是单调函数,求实数 的取值范围.
的取值范围.
(Ⅰ)详见解析; (Ⅱ)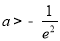
【解析】
试题分析:(Ⅰ) 当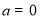 时,
时, ,对函数进行求导,求出函数的单调区间,即可求出函数的最小值,又由于
,对函数进行求导,求出函数的单调区间,即可求出函数的最小值,又由于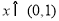 ,
,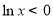 ,即可得到结论;(Ⅱ)由
,即可得到结论;(Ⅱ)由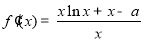 ,设
,设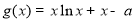 .令
.令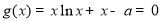 ,即
,即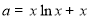 ,设函数
,设函数 .求出
.求出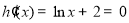 的解为
的解为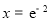 .然后再利用导数 求出函数的单调区间和函数的极值,即可求出结果.
.然后再利用导数 求出函数的单调区间和函数的极值,即可求出结果.
试题解析:【解析】
(Ⅰ) 当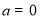 时,
时, ,
, .
.
令 ,解得
,解得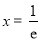 .
.
当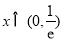 时,
时,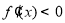 ,所以函数
,所以函数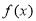 在
在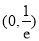 是减函数;
是减函数;
当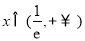 时,
时,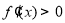 ,所以函数
,所以函数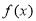 在
在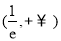 为增函数.
为增函数.
所以函数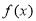 在
在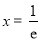 处取得最小值,
处取得最小值,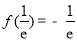 .
.
因为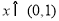 ,
,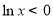 ,所以对任意
,所以对任意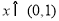 ,都有
,都有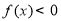 .
.
即对任意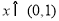 ,
,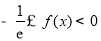 . 6分
. 6分
(Ⅱ)函数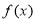 的定义域为
的定义域为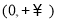 .
.
又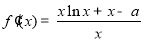 ,设
,设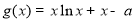 .
.
令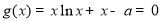 ,即
,即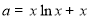 ,设函数
,设函数 .
.
令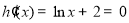 ,则
,则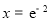 .
.
当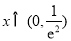 时,
时,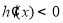 ,所以
,所以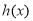 在
在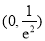 上是减函数;
上是减函数;
当 时,
时, ,所以
,所以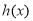 在
在 上是增函数;
上是增函数;
所以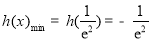 .则
.则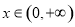 时,
时,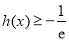 .
.
于是,当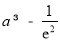 时,直线
时,直线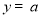 与函数
与函数 的图象有公共点,
的图象有公共点,
即函数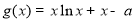 至少有一个零点,也就是方程
至少有一个零点,也就是方程 至少有一个实数根.
至少有一个实数根.
当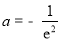 时,
时,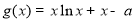 有且只有一个零点,
有且只有一个零点,
所以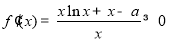 恒成立,函数
恒成立,函数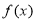 为单调增函数,不合题意,舍去.
为单调增函数,不合题意,舍去.
即当 时,函数
时,函数 不是单调增函数.
不是单调增函数.
又因为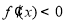 不恒成立,
不恒成立,
所以 为所求. 13分.
为所求. 13分.
考点: 1.利用导数研究函数的单调性.2.导数在证明不等式中的应用.


科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数f(x)的单调增区间.
(2)对任意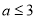 ,使得f(1)是函数f(x)在区间
,使得f(1)是函数f(x)在区间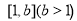 上的最大值,求实数 b 的取值范围.
上的最大值,求实数 b 的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在
在 上的最大值与最小值.
上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试文科数学试卷(解析版) 题型:选择题
若函数 的图象与
的图象与 轴交于点
轴交于点 ,过点
,过点 的直线
的直线 与函数的图象交于
与函数的图象交于 、
、 两点,则
两点,则 (其中O为坐标原点) ( )
(其中O为坐标原点) ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一文科数学试卷(解析版) 题型:选择题
已知函数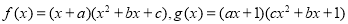 ,集合
,集合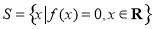 ,
,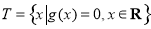 ,记
,记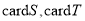 分别为集合
分别为集合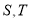 中的元素个数,那么下列结论不正确的是( )
中的元素个数,那么下列结论不正确的是( )
A.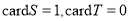 B.
B.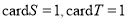
C.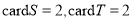 D.
D.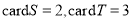
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com