
分析 由已知可得函数正确为6,再由已知求出f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1,然后利用周期概念得答案.
解答 解:由$f(x+3)=-\frac{1}{f(x)}$,得f(x+3+3)=-$\frac{1}{f(x+3)}$=$-\frac{1}{-\frac{1}{f(x)}}=f(x)$,即f(x+6)=f(x),
∴函数f(x)是周期为6的周期函数,
又当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x,
∴f(1)=1,f(2)=2,f(3)=f(-3)=-(-3+2)2=-1,f(4)=f(-2)=-(-2+2)2=0,f(5)=f(-1)=-1,f(6)=f(0)=0.
则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1,
则f(1)+f(2)+f(3)+…+f(2015)=335×1+f(1)+f(2)+f(3)+f(4)+f(5)=336.
故答案为:336.
点评 本题考查函数周期性的求法,由已知求出函数周期是解答该题的关键,是中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
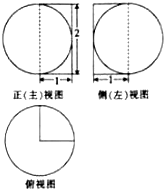
| A. | 2+π | B. | $\frac{4}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
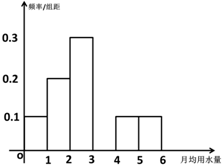 我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:
我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) | a | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.10 |
| [5,6) | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (0,1) | C. | $({\frac{1}{2},-\frac{1}{2}})$ | D. | $({-\frac{1}{2},-\frac{1}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com