
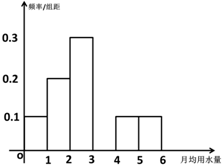
 我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:
我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) | a | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.10 |
| [5,6) | 10 | 0.10 |
| 合计 | 100 | 1.00 |
分析 (1)由频率分布表的性质能求出a,b.
(2)由频率分布表能作出频率分布图,由频率分直方图得[2,3)的小矩形最高,由此能求出众数,由[0,2)的频率为0.1+0.2=0.3,[2,3)的频率为0.3,能求出中位数,再由频率分布图能求出平均数.
解答 解:(1)由频率分布表得10+a+20+30+10+10=100,
解得a=20,
再由0.1+a+0.2+0.3+b+0.1+0.1=1,
得b=0.2.
(2)补充频率分布图如图: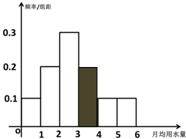
由频率分直方图得[2,3)的小矩形最高,∴众数为:2.5,
∵[0,2)的频率为0.1+0.2=0.3,[2,3)的频率为0.3,
∴中位数为:2+$\frac{0.5-0.3}{0.3}×$1≈2.67.
平均数为:0.1×0.5+0.2×1.5+0.3×2.5+0.2×3.5+0.1×4.5+0.1×5.5=2.8.
点评 本题考查实数a,b的求法,考查频率分布直方图的作法,考查众数、中位数、平均数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R2越大,线性相关系数r越小 | |
| B. | R2越小,线性相关系数越小 | |
| C. | R2越大,线性相关程度越小,R2越接近0,线性先关程度越大 | |
| D. | R2≥0且R2越接近1,线性相关程度越大,R2越接近0,线性相关程度越小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{{3-2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
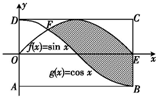 如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )| A. | $\frac{1+\sqrt{2}}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{1+\sqrt{2}}{2π}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com