
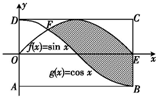
 如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )| A. | $\frac{1+\sqrt{2}}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{1+\sqrt{2}}{2π}$ | D. | $\frac{1}{2π}$ |
分析 利用定积分计算公式,算出曲线y=sinx与y=cosx围成的区域包含在区域D内的图形面积为S=2π,再由定积分求出阴影部分的面积,利用几何概型公式加以计算即可得到所求概率.
解答 解:根据题意,可得曲线y=sinx与y=cosx围成的区域,
其面积为∫${\;}_{\frac{π}{4}}^{π}$(sinx-cosx)dx=(-cosx-sinx)|${\;}_{\frac{π}{4}}^{π}$=1+$\sqrt{2}$;
又矩形ABCD的面积为2π,
由几何概型概率公式得该点落在阴影区域内的概率是$\frac{1+\sqrt{2}}{2π}$.
故选:C.
点评 本题给出区域和正余弦曲线围成的区域,求点落入指定区域的概率.着重考查了定积分计算公式、定积分的几何意义和几何概型计算公式等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
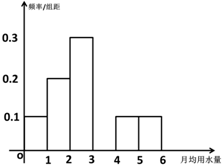 我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:
我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) | a | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.10 |
| [5,6) | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.
如图,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com