
分析 (1)先利用两角和余差的基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(2)x∈[-$\frac{π}{12}$,$\frac{5π}{12}}$)时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的取值范围.
解答 解:f(x)=$\frac{{\sqrt{3}}}{2}$cos2x+sin2(x+$\frac{π}{4}}$).
?f(x)=$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}-\frac{1}{2}cos(2x+\frac{π}{2})$
?f(x)=$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}$sin2x+$\frac{1}{2}$
?f(x)=sin(2x+$\frac{π}{3}$)+$\frac{1}{2}$,
(1)最小正周期$T=\frac{2π}{ω}=\frac{2π}{2}=π$,
∵sinx单调递增区间为[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],(k∈Z)
∴2x$+\frac{π}{3}$∈[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],(k∈Z)
解得:x∈[$kπ-\frac{5π}{12}$,$kπ+\frac{π}{12}$],(k∈Z)
∴f(x)的最小正周期为π;单调递增区间为[$kπ-\frac{5π}{12}$,$kπ+\frac{π}{12}$],(k∈Z)
(2)由(1)得:f(x)=sin(2x+$\frac{π}{3}$)+$\frac{1}{2}$
∵x∈[-$\frac{π}{12}$,$\frac{5π}{12}}$),
∴2x$+\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
由三角函数的图象和性质:
可知:当2x$+\frac{π}{3}$=$\frac{7π}{6}$时,f(x)取得最小值,即$f(x)_{min}=sin\frac{7π}{6}+\frac{1}{2}$=0.
当2x$+\frac{π}{3}$=$\frac{π}{2}$时,f(x)取得最大值,即$f(x)_{max}=sin\frac{π}{2}+\frac{1}{2}=\frac{3}{2}$.
∴x∈[-$\frac{π}{12}$,$\frac{5π}{12}}$)时,f(x)的取值范围在$[0,\frac{3}{2}]$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{{3-2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
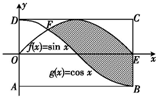 如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
如图,正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )| A. | $\frac{1+\sqrt{2}}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{1+\sqrt{2}}{2π}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
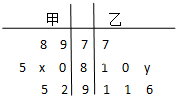 某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 168 | C. | 9 | D. | 169 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com