练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．过抛物线y2=4x的焦点F的直线分别交抛物线于A，B两点，交直线x=-1于点P．若$\overrightarrow{PA}$=λ$\overrightarrow{AF}$，$\overrightarrow{PB}$=μ$\overrightarrow{BF}$（λ，μ∈R），则λ+μ=0．

    分析 设A，B在准线上的射影分别为C，D，则|AC|=|AF|，|BD|=|BF|，利用$\overrightarrow{PA}$=λ$\overrightarrow{AF}$，$\overrightarrow{PB}$=μ$\overrightarrow{BF}$，可得|PA|=-λ|AC|，|PB|=μ|BD|，利用三角函数的定义，即可得出结论．

    解答 解：设A，B在准线上的射影分别为C，D，则|AC|=|AF|，|BD|=|BF|，
    ∵$\overrightarrow{PA}$=λ$\overrightarrow{AF}$，$\overrightarrow{PB}$=μ$\overrightarrow{BF}$，
    ∴|PA|=-λ|AC|，|PB|=μ|BD|，
    ∴-λ=$\frac{1}{cos∠CAP}$，μ=$\frac{1}{cos∠DBP}$，
    ∵∠CAP=∠DBP，
    ∴λ+μ=0．
    故答案为：0．

    点评 本题考查抛物线的定义，考查向量知识的运用，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．设函数f（x）=$\frac{{\sqrt{3}}}{2}$cos2x+sin2（x+$\frac{π}{4}}$）．
    （Ⅰ）求f（x）的最小正周期和单调递增区间；
    （Ⅱ）当x∈[-$\frac{π}{12}$，$\frac{5π}{12}}$）时，求f（x）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若关于x的方程（1-m）x2+2mx-1=0的所有根都是正实数，则实数m的取值范围是m≥1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知f（x）=$\left\{\begin{array}{l}{2（x＞1）}\\{-1（x≤1）}\end{array}\right.$，则不等式x+2xf（x+1）＞5的解集为（　　）
    A．（1，+∞）B．（-∞，-5）∪（1，+∞）C．（-∞，-5）∪（0，+∞）D．（-5，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

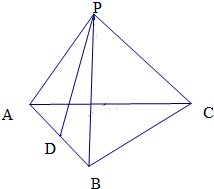    14．如图，三棱锥P-ABC的棱长都相等，D是棱AB的中点，则直线PD与直线BC所成角的余弦值为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{3}$C．$\frac{\sqrt{3}}{6}$D．$\frac{\sqrt{6}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．如图，在直二面角E-AB-C中，四边形ABEF是矩形，AB=2，AF=2$\sqrt{3}$，△ABC是以A为直角顶点的等腰直角三角形，点P是线段BF上的一点，PF=3．
    （Ⅰ）证明：BF⊥面PAC；
    （Ⅱ）求二面角A-BC-P的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=sin（${\frac{π}{2}$-x）sinx-$\sqrt{3}$cos2x．
    （1）求f（x）的单调递增区间；
    （2）若x∈[${\frac{π}{6}$，$\frac{2π}{3}}$]，求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某书店的销售刚刚上市的某知名品牌的高三数学单元卷，按事先限定的价格进行5天试销，每种单价试销1天，得到如表数据：
    单价x（元）1819202122
    销量y（册）6150504845
    （1）求试销5天的销售量的方差和y对x的回归直线方程；
    （2）预计今后的销售中，销售量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，为了获得最大利润，该单元卷的单价应定为多少元？
    （附：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-x）（{y}_{i}-y）}{\sum_{i=1}^{n}（{x}_{i}-x）}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}\overline{x}$））

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若函数f（x）=x2+a|x-$\frac{1}{2}$|在[0，+∞）上单调递增，则实数a的取值范围是（　　）
    A．[-2，0]B．[-4，0]C．[-1，0]D．[-$\frac{1}{2}$，0]

    查看答案和解析>>

    同步练习册答案