
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 50 | 50 | 48 | 45 |
分析 (1)计算平均数,利用公式求出a,b,即可得出y对x的回归直线方程;
(2)设工厂获得的利润为z元,利用利润=销售收入-成本,建立函数,利用配方法可求工厂获得的利润最大.
解答 解:(1)由题意,$\overline{x}$=20,$\overline{y}$=52,
∴$\stackrel{∧}{b}$=$\frac{-40}{10}$=-4,$\stackrel{∧}{a}$=52+20×4=132,
∴$\stackrel{∧}{y}$=-4x+132.
试销5天的销售量的方差=$\frac{1}{5}({9}^{2}+{4}^{2}+{2}^{2}+{4}^{2}+{7}^{2})$=33.2;
(2)获得的利润z=(x-14)(-4x+132)=-4x2+188x-1848,
函数的对称轴为x=23.5,开口向下,∴x=23.5元时,获得最大利润.
点评 本题主要考查回归分析,考查二次函数,考查运算能力、应用意识,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
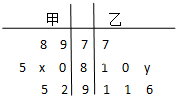 某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高一年级从甲、乙两个班各选出7名学生参加国防知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 168 | C. | 9 | D. | 169 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
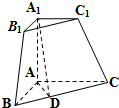 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{26}{27}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{23}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )
如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com