
分析 由已知a,b,c成等差数列结合正弦定理可得,2sinB=sinA+sinC利用和差化积公式可得,2sinA=2sin$\frac{B-C}{2}$,再利用半角公式及诱导进行化简,然后结合三角函数的性质即可得解.
解答 解:∵2a=b+c,
由正弦定理可得,2sinA=sinB+sinC,
则2sinA=2sin$\frac{B+C}{2}$cos$\frac{B-C}{2}$,
∴2sin$\frac{A}{2}$cos$\frac{A}{2}$=sin$\frac{π-A}{2}$cos$\frac{B-C}{2}$,
∴2sin$\frac{A}{2}$cos$\frac{A}{2}$=cos$\frac{A}{2}$cos$\frac{B-C}{2}$,
∴2sin$\frac{A}{2}$=cos$\frac{B-C}{2}$,
∵-1≤cos$\frac{B-C}{2}$≤1且sin$\frac{A}{2}$>0,
从而可得,0<sin$\frac{A}{2}$≤$\frac{1}{2}$,
∴0<$\frac{A}{2}$≤$\frac{π}{6}$,
∴0<A≤$\frac{π}{3}$.
故答案为:(0,$\frac{π}{3}$].
点评 本题主要考查了正弦定理的变形形式a=2RsinA,b=2RsinB,c=2RsinC的应用,和差角公式的变形及诱导公式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-5)∪(1,+∞) | C. | (-∞,-5)∪(0,+∞) | D. | (-5,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 50 | 50 | 48 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
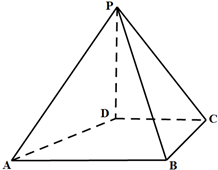 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥CD,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥CD,∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(人) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [-4,0] | C. | [-1,0] | D. | [-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com