练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．关于相关指数R2，下列说法正确的是（　　）
    A．R2越大，线性相关系数r越小
    B．R2越小，线性相关系数越小
    C．R2越大，线性相关程度越小，R2越接近0，线性先关程度越大
    D．R2≥0且R2越接近1，线性相关程度越大，R2越接近0，线性相关程度越小

    分析 根据相关指数R2，越接近于1时线性相关程度越大，模型的拟合效果越好，R2越接近0时，线性相关程度越小，即可判断结果．

    解答 解：相关指数R2用来刻画回归的效果，在含有一个解释变量的线性模型中，R2恰好等于相关系数r的平方．
    R2取值越大，意味着残差平方和越小，也就是模型的拟合效果越好；
    所以，相关指数R2≥0且R2越接近1，线性相关程度越大，R2越接近0，线性相关程度越小，D正确．
    故选：D．

    点评 本题主要考查了相关指数、线性相关系数的范围和两变量的线性相关性，及线性回归方程中的系数等概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知{an}是公差为4的等差数列，Sn是其前n项和．若S5=15，则a10的值是（　　）
    A．11B．20C．29D．31

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若函数y=sinωx能够在某个长度为1的区间上至少两次获得最大值1，且区间[-$\frac{π}{16}$，$\frac{π}{15}$]上为增函数，则正整数ω的值为（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．cos（-60°）的值等于（　　）
    A．$-\frac{1}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{1}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．圆x2+y2-4x=0的圆心坐标和半径分别（2，0），2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在△ABC中，若$A=\frac{π}{3}，tanB=\frac{1}{2}，AB=2\sqrt{3}+1$，则BC=$\sqrt{15}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

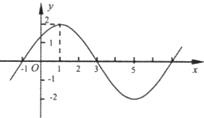    7．（1）已知函数$f（x）=Asin{（ωx+φ）_{\;}}（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的图象的一部分如图所示．求函数f（x）的解析式；
    （2）已知f（x）=$sin（2x+\frac{π}{6}）$+$\frac{3}{2}$，x∈R．函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样变换得到？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

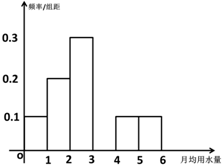    4．我国是严重缺水的国家之一，某市为了节约生活用水，计划在本市试行居民生活用水定额管理．为了较为合理地确定居民日常用水的标准，有关部门抽样调查了100位居民．如表是这100位居民月均用水量（单位：吨）的频率分布表，根据如表解答下列问题：
    （1）求表中a，b的值；
    分组频数频率
    [0，1）100.10
    [1，2）a0.20
    [2，3）300.30
    [3，4）20b
    [4，5）100.10
    [5，6）100.10
    合计1001.00
    （2）根据直方图估计该市每位居民月均用水量的众数、中位数、平均数．（在试卷上将下面的频率分布直方图补充完整）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知样本数为11，计算得$\sum_{i=1}^{11}{x_i}=66$，$\sum_{i=1}^{11}{y_i}=132$，回归方程为y=0.3x+a，则a=10.2．

    查看答案和解析>>

    同步练习册答案