
分析 (1)先利用二倍角将函数化为y=Asin(ωx+φ)+B的形式,再利用周期公式求函数的最小正周期,最后将内层函数看作整体,放到正弦函数的减区间上,解不等式得函数的单调递减区间;
(2)结合三角函数的图象和性质,求出f(x)最大和最小值,并解出对应的x值.
解答 解:由$f(x)=sin\frac{x}{2}cos\frac{x}{2}+{cos^2}\frac{x}{2}-1$.
?f(x)=$\frac{1}{2}$sinx+$\frac{1}{2}$$+\frac{1}{2}$cosx-1
?f(x)=$\frac{1}{2}$sinx+$\frac{1}{2}$cosx-$\frac{1}{2}$
?f(x)=$\frac{\sqrt{2}}{2}sin(x+\frac{π}{4})-\frac{1}{2}$,
(1)∴f(x)的最小正周期$T=\frac{2π}{ω}=\frac{2π}{1}=2π$.
∵y=sinx函数的单调递减区间为$[2kπ+\frac{π}{2},2kπ+\frac{3π}{2}]$,(k∈Z)
∴$x+\frac{π}{4}∈$$[2kπ+\frac{π}{2},2kπ+\frac{3π}{2}]$,(k∈Z)
解得:$2kπ+\frac{π}{4}≤x≤2kπ+\frac{5π}{4}$,(k∈Z)
∴f(x)的单调递减区间为$[2kπ+\frac{π}{4},2kπ+\frac{5π}{4}]$,(k∈Z)
(2)由三角函数的图象和性质:
可知:当∴$x+\frac{π}{4}=\frac{π}{2}+2kπ$时,f(x)取得最大值,即:$f(x)_{max}=\frac{\sqrt{2}}{2}-\frac{1}{2}=\frac{\sqrt{2}-1}{2}$;
此时解得$x=2kπ+\frac{π}{4}$,(k∈Z)
当$x+\frac{π}{4}=-\frac{π}{2}+2kπ$时,f(x)取得最小值,即:$f(x)_{min}=-\frac{\sqrt{2}}{2}-\frac{1}{2}=-\frac{\sqrt{2}+1}{2}$;
此时解得$x=2kπ-\frac{3π}{4}$,(k∈Z)
点评 本题考查了利用二倍角化简三角函数的能力和三角函数的图象和性质的运用能力.属于基础题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
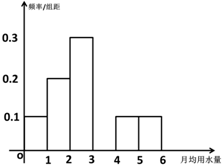 我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:
我国是严重缺水的国家之一,某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较为合理地确定居民日常用水的标准,有关部门抽样调查了100位居民.如表是这100位居民月均用水量(单位:吨)的频率分布表,根据如表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) | a | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.10 |
| [5,6) | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (0,1) | C. | $({\frac{1}{2},-\frac{1}{2}})$ | D. | $({-\frac{1}{2},-\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com