
���� ��1����ȥ�������ɵ�ֱ��l��ֱ�����귽�̣����ü�������ֱ������Ļ����������ɵ�ԲC��ֱ�����귽�̣�
��2����P��Բ��C�ľ�����Сʱ��PC��l�������ʱPC�ķ��̣���y=$\sqrt{3}$��x-3���������ɵ�P�����꣮
��� �⣺��1��ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=3+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$��tΪ��������ֱ�����귽��Ϊy=$\sqrt{3}$��x-3����
ԲC�ļ����귽��Ϊ$��=2\sqrt{3}sin��$��ֱ�����귽��x2+y2-2$\sqrt{3}$y=0��
��2����P��Բ��C�ľ�����Сʱ��PC��l����ʱPC�ķ���Ϊy-$\sqrt{3}$=-$\frac{\sqrt{3}}{3}$x��
��y=$\sqrt{3}$��x-3���������ɵ�P��3��0����
���� ���⿼�����������ֱ�����귽�̣���������ֱ�����귽�̵Ļ���������ѧ���ļ����������Ƚϻ�����


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
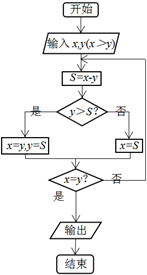
| A�� | 2849 | B�� | 37 | C�� | 74 | D�� | 77 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $-\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
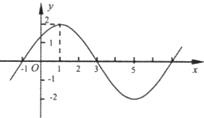 ��1����֪����$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$��ͼ���һ������ͼ��ʾ������f��x���Ľ���ʽ��
��1����֪����$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$��ͼ���һ������ͼ��ʾ������f��x���Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
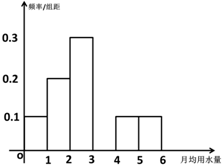 �ҹ�������ȱˮ�Ĺ���֮һ��ij��Ϊ�˽�Լ������ˮ���ƻ��ڱ������о���������ˮ���������Ϊ�˽�Ϊ������ȷ�������ճ���ˮ�ı����йز��ų���������100λ�����������100λ�����¾���ˮ������λ���֣���Ƶ�ʷֲ����������������������⣺
�ҹ�������ȱˮ�Ĺ���֮һ��ij��Ϊ�˽�Լ������ˮ���ƻ��ڱ������о���������ˮ���������Ϊ�˽�Ϊ������ȷ�������ճ���ˮ�ı����йز��ų���������100λ�����������100λ�����¾���ˮ������λ���֣���Ƶ�ʷֲ����������������������⣺| ���� | Ƶ�� | Ƶ�� |
| [0��1�� | 10 | 0.10 |
| [1��2�� | a | 0.20 |
| [2��3�� | 30 | 0.30 |
| [3��4�� | 20 | b |
| [4��5�� | 10 | 0.10 |
| [5��6�� | 10 | 0.10 |
| �ϼ� | 100 | 1.00 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��0�� | B�� | ��0��1�� | C�� | $��{\frac{1}{2}��-\frac{1}{2}}��$ | D�� | $��{-\frac{1}{2}��-\frac{1}{2}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com