
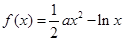 ,
,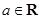 .
. 的单调区间;
的单调区间; 在区间
在区间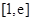 的最小值为
的最小值为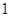 ,求
,求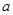 的值.
的值. 时,函数
时,函数 的单调减区间是
的单调减区间是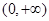 ,当
,当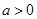 时,函数
时,函数 的单调减区间是
的单调减区间是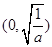 ,单调增区间为
,单调增区间为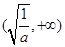 ;(2)
;(2)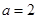 .
.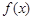 的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数
的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数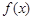 的单调区间,求函数
的单调区间,求函数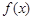 导函数
导函数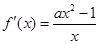 ,令
,令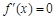 ,找出分界点,从而确定函数的单调区间,但由于含有参数
,找出分界点,从而确定函数的单调区间,但由于含有参数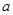 ,需对参数
,需对参数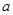 分
分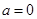 ,
,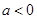 ,
,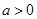 讨论,从而得函数
讨论,从而得函数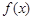 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间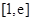 的最小值为
的最小值为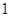 ,求
,求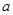 的值,求出函数
的值,求出函数 在区间
在区间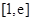 的最小值,令它等于为
的最小值,令它等于为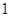 即可,由(1)可知,当
即可,由(1)可知,当 时,函数
时,函数 的单调减区间是
的单调减区间是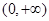 ,
, 的最小值为
的最小值为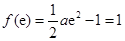 ,解出
,解出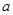 ,验证是否符合,当
,验证是否符合,当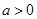 时,函数
时,函数 的单调减区间是
的单调减区间是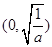 ,单调增区间为
,单调增区间为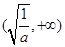 ,由于不知函数
,由于不知函数 在区间
在区间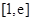 的单调性,需讨论
的单调性,需讨论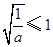 ,
,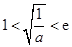 ,
,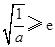 ,分别求出函数
,分别求出函数 在区间
在区间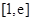 的最小值,令它等于为
的最小值,令它等于为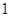 ,解出
,解出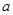 ,验证是否符合,从而得
,验证是否符合,从而得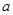 的值.
的值. 的定义域是
的定义域是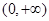 ,
, 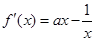
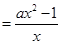 .
.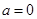 时,
时,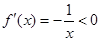 ,故函数
,故函数 在
在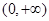 上单调递减.
上单调递减.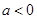 时,
时,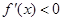 恒成立,所以函数
恒成立,所以函数 在
在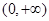 上单调递减.
上单调递减.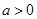 时,令
时,令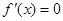 ,又因为
,又因为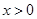 ,解得
,解得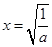 .
.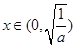 时,
时,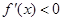 ,所以函数
,所以函数 在
在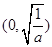 单调递减.
单调递减. 时,
时,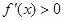 ,所以函数
,所以函数 在
在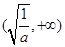 单调递增.
单调递增. 时,函数
时,函数 的单调减区间是
的单调减区间是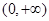 ,
,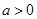 时,函数
时,函数 的单调减区间是
的单调减区间是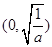 ,单调增区间为
,单调增区间为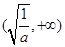 . 7分
. 7分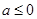 时,由(1)可知,
时,由(1)可知, 在
在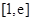 上单调递减,
上单调递减, 的最小值为
的最小值为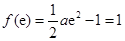 ,解得
,解得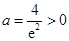 ,舍去.
,舍去.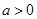 时,由(1)可知,
时,由(1)可知,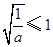 ,即
,即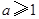 时,函数
时,函数 在
在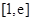 上单调递增,
上单调递增, 的最小值为
的最小值为 ,解得
,解得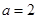 .
.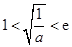 ,即
,即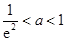 时,函数
时,函数 在
在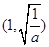 上单调递减,
上单调递减,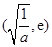 上单调递增,所以函数
上单调递增,所以函数 的最小值为
的最小值为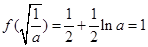 ,解得
,解得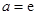 ,舍去.
,舍去.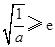 ,即
,即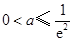 时,函数
时,函数 在
在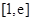 上单调递减,
上单调递减, 的最小值为
的最小值为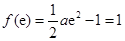 ,得
,得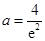 ,舍去.
,舍去.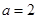 . 13分
. 13分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com