
 .
. 的单调区间;
的单调区间; 时,求证:
时,求证: 恒成立..
恒成立..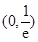 ,单调增区间为
,单调增区间为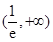 ,(2)详见解析.
,(2)详见解析.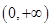 ,二是求导数为零的根,由
,二是求导数为零的根,由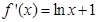 得
得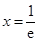 ,三是分区间讨论导数正负,当
,三是分区间讨论导数正负,当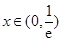 时,
时,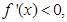 当
当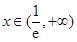 时,
时,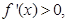 四是根据导数正负写出单调区间:单调减区间为
四是根据导数正负写出单调区间:单调减区间为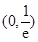 ,单调增区间为
,单调增区间为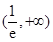 ,.(2)证明不等式恒成立问题一般化为函数最值问题.可以直接求函数
,.(2)证明不等式恒成立问题一般化为函数最值问题.可以直接求函数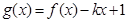 的最小值,也可
的最小值,也可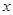 将
将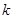 与分离,求函数
与分离,求函数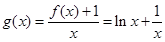 的最小值.两种思路都简洁,实质都一样,就是求最小值.
的最小值.两种思路都简洁,实质都一样,就是求最小值.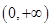 1分
1分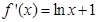 2分
2分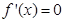 ,得
,得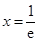 3分
3分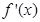 与
与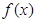 的情况如下:
的情况如下: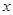 |  |  | 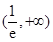 |
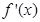 | 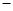 | 0 | 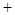 |
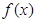 | ↘ | 极小值 | ↗ |
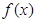 的单调减区间为
的单调减区间为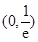 ,单调增区间为
,单调增区间为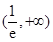 6分
6分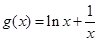 ,
,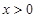 7分
7分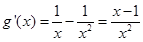 8分
8分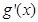 与
与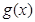 的情况如下:
的情况如下: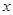 | 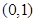 | 1 |  |
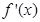 | 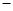 | 0 | 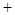 |
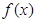 | ↘ | 极小值 | ↗ |
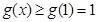 ,即
,即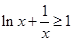 在
在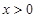 时恒成立, 10分
时恒成立, 10分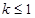 时,
时,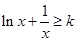 ,
,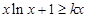 ,即
,即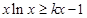 ,
,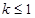 时,有
时,有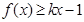 . 13分
. 13分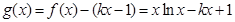 7分
7分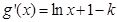 8分
8分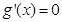 ,得
,得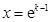 9分
9分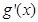 与
与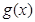 的情况如下:
的情况如下: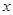 | 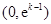 | 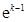 | 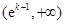 |
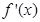 | 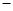 | 0 | 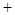 |
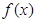 | ↘ | 极小值 | ↗ |
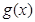 的最小值为
的最小值为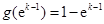 -11分
-11分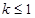 时,
时,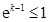 ,所以
,所以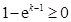
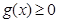 -12分
-12分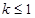 时,
时,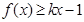 . 13分
. 13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求f(x)在[-1,1]上的最小值;
,求f(x)在[-1,1]上的最小值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com