
(08年安庆市二模)(14分)若![]() ,
,![]() 分别为双曲线
分别为双曲线![]() 的左右焦点,O为坐标原点,P在双曲线的左支上,M在右准线上,且满足
的左右焦点,O为坐标原点,P在双曲线的左支上,M在右准线上,且满足![]() ,
,![]()
(1)求此双曲线的离心率;
(2)若此双曲线过点![]() ,求该双曲线的方程;
,求该双曲线的方程;
(3)设(2)中双曲线的虚轴端点为![]() 、
、![]() (
(![]() 在y轴正半轴上),是否存在经过点
在y轴正半轴上),是否存在经过点![]() 的直线l与双曲线交于A,B两点,且以AB为直径的圆过点
的直线l与双曲线交于A,B两点,且以AB为直径的圆过点![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
(08年安庆市二模) (14分)如图,正三棱柱![]() 所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H。
所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H。
(1)求证:AE⊥平面A1BD;
(2)求二面角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)求点B1到平面A1BD的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安庆市二模理)(13分)安庆驾校最近出台了一项机动车驾照考试的规定:要求每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,便可以领取驾照,不再参加以后的考试,对于四次考试都未通过者,须进入下一年度的考核。如果李明决定参加驾照考试,假设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9。
(1)求在一年内李明参加驾照考试次数![]() 的分布列和
的分布列和![]() 的期望;
的期望;
(2)求李明在一年内领到驾照的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安庆市二模理) (14分)如图,![]() 是棱长为1的正方体,
是棱长为1的正方体,![]() 是四棱锥,且
是四棱锥,且![]() 平面
平面![]() ,
,![]() 。
。
(1)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(2)求证:直线![]() 平行于平面
平行于平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
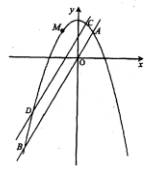
(08年安庆市二模理)(12分) 设点A、B是直线![]() 与抛物线
与抛物线![]() 的两个交点,抛物线上的动点M在A、B两点间移动,如图所示。
的两个交点,抛物线上的动点M在A、B两点间移动,如图所示。
(1)试求M的坐标,使得△MAB的面积最大;
(2)试证明:抛物线![]() 上平行于AB的弦恒被一条定直线平分。
上平行于AB的弦恒被一条定直线平分。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com