
【题目】设命题![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() ,命题
,命题![]() 实数
实数![]() 满足
满足![]() .
.
(1)若![]() ,有
,有![]() 且
且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)x∈(2,3);(2)(1,2].
【解析】试题分析:(1)命题p:实数x满足![]() ,其中
,其中![]() >0,解得
>0,解得![]() <x<3
<x<3![]() .若
.若![]() =1,则p中:1<x<3,由p且q为真,可得p与q都为真,即可得出.
=1,则p中:1<x<3,由p且q为真,可得p与q都为真,即可得出.
(2)若p是q的充分不必要条件,可得q是p 的充分不必要条件,即可得出.
试题解析:
(1)命题p:实数x满足(x-a)(x-3a)<0,其中a>0,解得a<x<3a.
命题q中:实数x满足 2<x≤3. 若a=1,则p中:1<x<3,
∵p且q为真,∴![]() ,解得2<x<3, 故所求x∈(2,3).
,解得2<x<3, 故所求x∈(2,3).
(2)若p是q的充分不必要条件, 则q是p 的充分不必要条件,
∴![]() ,解得1<a≤2, ∴a的取值范围.是(1,2]
,解得1<a≤2, ∴a的取值范围.是(1,2]


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: 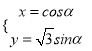 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直角坐标系下曲线![]() 与曲线
与曲线![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最大值,并求此时点
上点的距离的最大值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数),若
为参数),若![]() 是圆
是圆![]() 与
与![]() 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,设过点
轴正半轴为极轴,建立极坐标系,设过点![]() 的圆
的圆![]() 的切线为
的切线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)求圆![]() 上到直线
上到直线![]() 的距离最大的点的直角坐标.
的距离最大的点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中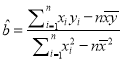 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;
(2)求该圆的半径r的取值范围;
(3)求圆心C的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com