
分析 (1)①由an+1=2an-1,可得an+1-1=2(an-1),利用等比数列的通项公式即可得出.
②假设{an}为“等比源数列”,则此数列中存在三项:ak<am<an,k<m<n.满足${a}_{m}^{2}$=akan,代入化为:2m-k+1(2m-2+1)=2n-1+2n-k+1,利用数的奇偶性即可得出.
(2)设等差数列{an}的公差为d,假设存在三项使得${a}_{n}^{2}={a}_{k}{a}_{m}$,(k<n<m).展开:2a1(n-1)+(n-1)2d=a1[(k-1)+(m-1)]+(k-1)(m-1)d,当n-1既是(k-1)与m-1的等比中项,又是(k-1)与m-1的等差中项时,原命题成立.
解答 解:(1)①∵an+1=2an-1,∴an+1-1=2(an-1),
∴数列{an-1}是等比数列,首项为1,公比为2.
∴an-1=2n-1,
∴an=2n-1+1.
②假设{an}为“等比源数列”,
则此数列中存在三项:ak<am<an,k<m<n.
满足${a}_{m}^{2}$=akan,
∴(2m-1+1)2=(2k-1+1)(2n-1+1),
化为:22m-2+2m=2k+n-2+2n-1+2k-1,
∴2m-k+1(2m-2+1)=2n-1+2n-k+1,
可知:左边为偶数,而右边为奇数,因此不可能成立.
故{an}不是“等比源数列”.
(2)设等差数列{an}的公差为d,
则an=a1+(n-1)d,a1≠0,an∈Z(n∈N*),
假设存在三项使得${a}_{n}^{2}={a}_{k}{a}_{m}$,(k<n<m).
∴$[{a}_{1}+(n-1)d]^{2}$=[a1+(k-1)d][a1+(m-1)d],
展开:2a1(n-1)+(n-1)2d=a1(k-1)+(m-1)+(k-1)(m-1)d,
当n-1既是(k-1)与m-1的等比中项,又是(k-1)与m-1的等差中项时,原命题成立.
点评 本题考查了等差数列与等比数列的通项公式及其性质、新定义“等比源数列”,考查了推理能力与计算能力,属于难题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
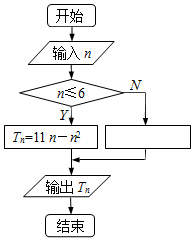 已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | [-2,-1) | C. | (-1,1) | D. | [-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
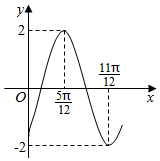
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com