
【题目】平行四边形![]() 所在的平面与直角梯形
所在的平面与直角梯形![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
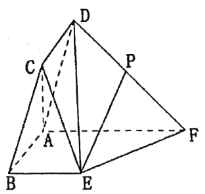
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)取![]() 的中点
的中点![]() 或取
或取![]() 中点
中点![]() ,利用证平行四边形的方法再证明
,利用证平行四边形的方法再证明![]() 平面
平面![]() 即可.
即可.
(2)根据勾股定理与余弦定理证明![]() ,再根据面面垂直的性质得出
,再根据面面垂直的性质得出![]() 平面
平面![]() 即可证明
即可证明![]() .
.
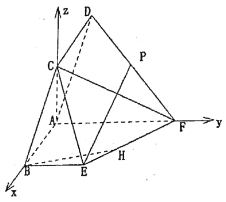
(3) 以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
设![]() ,再利用空间向量求解关于线面角的问题即可.
,再利用空间向量求解关于线面角的问题即可.
(1)解法1:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,
在直角梯形![]() 中,
中,![]() ,
,![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
在![]() 中
中![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

解法2:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
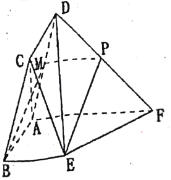
(2)在![]() 中
中![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() .
.
(3)由(1)(2)以![]() 为原点,以
为原点,以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
所以![]() ,
,
所以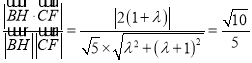 ,
,
所以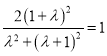 ,
,
所以![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以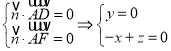 ,
,
所以令![]() ,则
,则![]() ,
,
如![]() 与平面
与平面![]() 成的角为
成的角为![]() ,
,
所以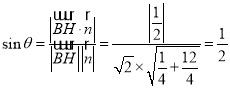 .
.
所以![]() ,即
,即![]() 与面
与面![]() 成的角为
成的角为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,正确的命题有________(填写正确的序号)
①若![]() ,则
,则![]() 的最小值是6;
的最小值是6;
②如果不等式![]() 的解集是
的解集是![]() ,那么
,那么![]() 恒成立;
恒成立;
③设x,![]() ,且
,且![]() ,则
,则![]() 的最小值是
的最小值是![]() ;
;
④对于任意![]() ,
,![]() 恒成立,则t的取值范围是
恒成立,则t的取值范围是![]() ;
;
⑤“![]() ”是“复数
”是“复数![]() (
(![]() )是纯虚数”的必要非充分条件;
)是纯虚数”的必要非充分条件;
⑥若![]() ,
,![]() ,
,![]() ,则必有
,则必有![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中,![]()
![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() . 点E在棱AB上,平面
. 点E在棱AB上,平面![]() 与棱
与棱![]() 相交于点F.
相交于点F.
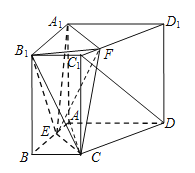
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)写出三棱锥![]() 体积的取值范围. (结论不要求证明)
体积的取值范围. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),每一件产品的销售价格定为
万元(不含促销费用),每一件产品的销售价格定为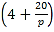 元,假定厂家的生产能力完全能满足市场的销售需求.
元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
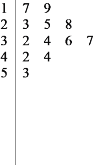
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;大于等于30万件且小于40万件,当月奖励该电商平台5万元;当月低于30万件没有奖励,用该样本估计总体,从电商平台一个年度内任取两个月,记这两个月企业发给电商平台的奖金为万元,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
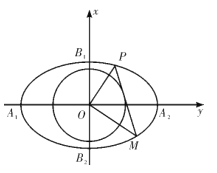
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
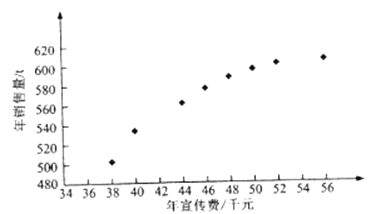
(![]() =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
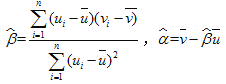
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
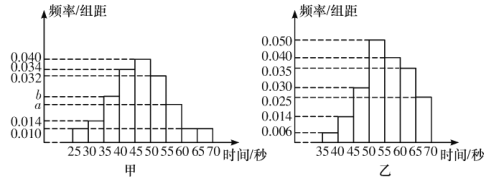
(1)若甲解开密码锁所需时间的中位数为47,求![]() 、
、![]() 的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.
②试猜想:该团队以怎样的先后顺序派出人员,可使所需派出的人员数目![]() 的数学期望达到最小,不需要说明理由.
的数学期望达到最小,不需要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com