
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
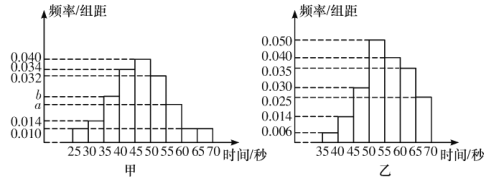
(1)若甲解开密码锁所需时间的中位数为47,求![]() 、
、![]() 的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.
②试猜想:该团队以怎样的先后顺序派出人员,可使所需派出的人员数目![]() 的数学期望达到最小,不需要说明理由.
的数学期望达到最小,不需要说明理由.
【答案】(1)![]() ;
;![]() ;甲在1分钟内解开密码锁的频率是
;甲在1分钟内解开密码锁的频率是![]() ;乙在1分钟内解开密码锁的频率是
;乙在1分钟内解开密码锁的频率是![]() (2)①按乙丙甲派出的顺序期望更小②先派出甲,再派乙,最后派丙
(2)①按乙丙甲派出的顺序期望更小②先派出甲,再派乙,最后派丙
【解析】
(1)根据甲解开密码锁所需时间的中位数求得![]() ,根据频率求得
,根据频率求得![]() ,由此求得甲在1分钟内解开密码锁的频率.通过频率分布直方图求得乙在1分钟内解开密码锁的频率.
,由此求得甲在1分钟内解开密码锁的频率.通过频率分布直方图求得乙在1分钟内解开密码锁的频率.
(2)
①分别求得两个不同顺序的方法对应的数学期望,由此求得期望更小的安排方法.
②按照解锁概率大的人员排前面,期望值最小.通过计算前两位、后两位人员交换时,期望值的变化情况,来确定最优的排法.
(1)甲解开密码锁所需时间的中位数为47,
∴![]()
![]() ,解得
,解得![]() ;
;
∴![]() ,解得
,解得![]() ;
;
∴甲在1分钟内解开密码锁的频率是![]() ;
;
乙在1分钟内解开密码锁的频率是![]() ;
;
(2)由(1)知,甲、乙、丙在1分钟内解开密码锁的概率分别是![]() ,
,![]() ,
,![]() 且各人是否解开密码锁相互独立;
且各人是否解开密码锁相互独立;
设按乙丙甲的顺序对应的数学期望为![]() ,按丙乙甲的顺序对应的数学期望为
,按丙乙甲的顺序对应的数学期望为![]()
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,∴
,∴![]() ,
,
①∴![]()
同理可求得![]()
所以按乙丙甲派出的顺序期望更小.
②答案:先派出甲,再派乙,最后派丙,
(下面是理由,给老师和学生参考)
设按先后顺序自能完成任务的概率分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 互不相等,
互不相等,
根据题意知![]() 的取值为1,2,3;
的取值为1,2,3;
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,∴
,∴![]() ,
,
若交换前两个人的派出顺序,则变为![]() ,
,
由此可见,当![]() 时,交换前两人的派出顺序会增大均值,故应选概率最大的甲先开锁;
时,交换前两人的派出顺序会增大均值,故应选概率最大的甲先开锁;
若保持第一人派出的人选不变,交换后两人的派出顺序,
∵交换前![]() ,
,
∴交换后的派出顺序则期望值变为![]() ,
,
当![]() 时,交换后的派出顺序可增大均值;所以先派出甲,再派乙,最后派丙,
时,交换后的派出顺序可增大均值;所以先派出甲,再派乙,最后派丙,
这样能使所需派出的人员数目的均值(教学期望)达到最小.


科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为1.
的面积的最大值为1.
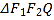
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() 且使
且使![]() 轴,如图,问四边形
轴,如图,问四边形![]() 的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() :实数
:实数![]() 满足不等式
满足不等式![]() ;命题
;命题![]() :函数
:函数![]() 有极值点.
有极值点.
(1)若![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,并记为
为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() :
:![]() 经过伸缩变换
经过伸缩变换![]() ,后得到曲线
,后得到曲线![]() 以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为
以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为![]()
![]() 求曲线
求曲线![]() 的直角坐标方程及直线l的直角坐标方程;
的直角坐标方程及直线l的直角坐标方程;
![]() 在
在![]() 上求一点M,使点M到直线l的距离最小,并求出最小距离.
上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由团中央学校部、全国学联秘书处、中国青年报社共同举办的2018年度全国“最美中学生“寻访活动结果出炉啦,此项活动于2018年6月启动,面向全国中学在校学生,通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”.现随机抽取了30名学生的票数,线成如图所示的茎叶图,若规定票数在65票以上(包括65票)定义为风华组.票数在65票以下(不包括65票)的学生定义为青春组.

(Ⅰ)在这30名学生中,青春组学生中有男生7人,风华组学生中有女生12人,试问有没有![]() 的把握认为票数分在青春组或风华组与性别有关;
的把握认为票数分在青春组或风华组与性别有关;
(Ⅱ)如果用分层抽样的方法从青春组和风华组中抽取5人,再从这5人中随机抽取2人,那么至少有1人在青春组的概率是多少?
(Ⅲ)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机选取4人,用![]() 表示所选4人中青春组的人数,试写出
表示所选4人中青春组的人数,试写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
附: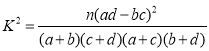 ;其中
;其中![]()
独立性检验临界表:
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com