
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递减.,
单调递减.,
当![]() 时,
时, ![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)证明见解析.
【解析】分析:(1)首先确定函数的定义域,之后对函数求导,之后对![]() 进行分类讨论,从而确定出导数在相应区间上的符号,从而求得函数对应的单调区间;
进行分类讨论,从而确定出导数在相应区间上的符号,从而求得函数对应的单调区间;
(2)根据![]() 存在两个极值点,结合第一问的结论,可以确定
存在两个极值点,结合第一问的结论,可以确定![]() ,令
,令![]() ,得到两个极值点
,得到两个极值点![]() 是方程
是方程![]() 的两个不等的正实根,利用韦达定理将其转换,构造新函数证得结果.
的两个不等的正实根,利用韦达定理将其转换,构造新函数证得结果.
详解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(i)若![]() ,则
,则![]() ,当且仅当
,当且仅当![]() ,
,![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
(ii)若![]() ,令
,令![]() 得,
得,![]() 或
或![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)由(1)知,![]() 存在两个极值点当且仅当
存在两个极值点当且仅当![]() .
.
由于![]() 的两个极值点
的两个极值点![]() 满足
满足![]() ,所以
,所以![]() ,不妨设
,不妨设![]() ,则
,则![]() .由于
.由于
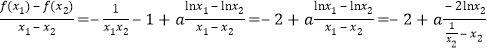 ,
,
所以![]() 等价于
等价于![]() .
.
设函数![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 单调递减,又
单调递减,又![]() ,从而当
,从而当![]() 时,
时,![]() .
.
所以![]() ,即
,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
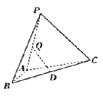
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕边AB翻转至
绕边AB翻转至![]() ,使面
,使面![]() 面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后,左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体的体积为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,左焦点为
,左焦点为![]() ,离心率为
,离心率为![]() ,不与坐标轴垂直的直线
,不与坐标轴垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)若![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
(2)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,设直线
,设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,问:
,问: ![]() 是否为定值?若是.请求出
是否为定值?若是.请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
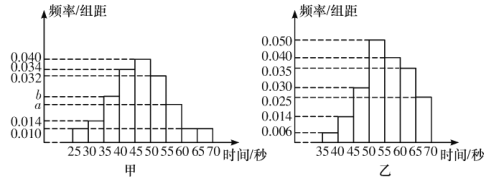
(1)若甲解开密码锁所需时间的中位数为47,求![]() 、
、![]() 的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.
②试猜想:该团队以怎样的先后顺序派出人员,可使所需派出的人员数目![]() 的数学期望达到最小,不需要说明理由.
的数学期望达到最小,不需要说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com