
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
【答案】![]()
【解析】
甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,另一种情形为从甲袋中取出的球是白球,放入乙袋,并由乙袋取白球放入甲.
甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,记作事件E,
此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,
另一种情形为从甲袋中取出的球是白球,放入乙袋,此事件用F1表示,
并由乙袋取白球放入甲,用F2表示,令F=F1F2.则所求事件为E∪F,且E与F互斥,
显然P(E)=![]() ,
,
下面计算P(F),记F1为由甲袋取出白球(不放入乙袋),F2为当乙袋内有5个白球,6个黑球时取出一球为白球,则显然有P(F1F2)=P(F1′F2′).而F1′与F2′独立,故P(F1′F2′)=![]() .∴P(E∪F)=P(E)+P(F)=
.∴P(E∪F)=P(E)+P(F)=![]() +
+![]() =
=![]()
故答案为:![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】设A,B分别为双曲线![]() (a>0,b>0)的左、右顶点,双曲线的实轴长为4
(a>0,b>0)的左、右顶点,双曲线的实轴长为4![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线y=![]() x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使
x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的1000名高三学生参加四门学科的选拔考试,每门试卷共有10道题,每题10分,规定:每门错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,在录取时,
,在录取时,![]() 记为90分,
记为90分,![]() 记为80分,
记为80分,![]() 记为60分,
记为60分,![]() 记为50分.
记为50分.
根据模拟成绩,每一门都有如下统计表:
答错 题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 90 | 100 | 150 | 150 | 200 | 100 | 100 | 50 | 49 | 1 |
已知选拔性考试成绩与模拟成绩基本吻合.
(1)设![]() 为高三学生一门学科的得分,求
为高三学生一门学科的得分,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)预测考生4门总分为320概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
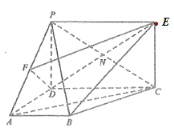
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在R上的偶函数且以2为周期,则“
是定义在R上的偶函数且以2为周期,则“![]() 为
为![]() 上的增函数”是“
上的增函数”是“![]() 为
为![]() 上的减函数”的
上的减函数”的![]()
![]()
A. 充分而不必要的条件B. 必要而不充分的条件
C. 充要条件D. 既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义两点![]() 与
与![]() 之间的“直角距离”为:
之间的“直角距离”为:![]() .现给出下列4个命题:
.现给出下列4个命题:
①已知![]() 、
、![]() ,则
,则![]() 为定值;
为定值;
②已知![]() 三点不共线,则必有
三点不共线,则必有![]() ;
;
③用![]() 表示
表示![]() 两点之间的距离,则
两点之间的距离,则![]() ;
;
④若![]() 是椭圆
是椭圆![]() 上的任意两点,则
上的任意两点,则![]() 的最大值为6.
的最大值为6.
则下列判断正确的为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数 z a bi ,其中 a .b 为实数,i 为虚数单位, ![]() 为 z 的共轭复数,且存在非零实数 t ,使
为 z 的共轭复数,且存在非零实数 t ,使![]() 成立.
成立.
(1)求 2a b 的值;
(2)若| z 2 | 5,求实数 a 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com