
【题目】已知复数 z a bi ,其中 a .b 为实数,i 为虚数单位, ![]() 为 z 的共轭复数,且存在非零实数 t ,使
为 z 的共轭复数,且存在非零实数 t ,使![]() 成立.
成立.
(1)求 2a b 的值;
(2)若| z 2 | 5,求实数 a 的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对 n N ,设抛物线 y2 2(2n 1) x ,过 P 2n, 0 任作直线 l 与抛物线交与 An, Bn两点,则数列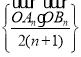 的前 n 项和为_____;
的前 n 项和为_____;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆 C : ![]()
![]() ,称圆心在原点,半径为
,称圆心在原点,半径为![]() 的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(
的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(![]() , 0) ,其短轴上的一个端点到 F1 的距离为
, 0) ,其短轴上的一个端点到 F1 的距离为![]()
(1)求椭圆 C 的方程及其“伴随圆”方程;
(2)若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点,且与椭圆 C 的伴随圆相交于 M .N 两点,求弦 MN 的的长;
(3)点 P 是椭圆 C 的伴随圆上一个动点,过点 P 作直线 l1、l2,使得 l1、l2与椭圆 C 都只有一个公共点,判断l1、l2的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球、两个“
”号球、两个“![]() ”号球、三个“
”号球、三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球、五个“
”号球、五个“![]() ”号球,每次摸奖后放回,消费额满
”号球,每次摸奖后放回,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金.
元,摸得无号球则没有奖金.
(Ⅰ)经统计,消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 为顾客,请估计消费额
为顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数;
内并中奖的人数;
(Ⅱ)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列;
的分布列;
(Ⅲ)某顾客消费额为![]() 元,有两种摸奖方法,方法一:三次
元,有两种摸奖方法,方法一:三次![]() 箱内摸奖机会;方法二:一次
箱内摸奖机会;方法二:一次![]() 箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
附:若![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
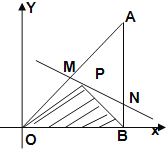
【题目】如图所示,将一块直角三角形板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角板锯成
将三角板锯成![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
(1)用![]() 表示出直线
表示出直线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标;
的坐标;
(2)求出![]() 的取值范围及其所对应的倾斜角
的取值范围及其所对应的倾斜角![]() 的范围;
的范围;
(3)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com