
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨΌ––¥ΌœζΜνΕ·Θ§”–ΝΫΗωΟΰΫ±œδΘ§![]() œδΡΎ”–“ΜΗωΓΑ
œδΡΎ”–“ΜΗωΓΑ![]() Γ±Κ≈«ρΓΔΝΫΗωΓΑ
Γ±Κ≈«ρΓΔΝΫΗωΓΑ![]() Γ±Κ≈«ρΓΔ»ΐΗωΓΑ
Γ±Κ≈«ρΓΔ»ΐΗωΓΑ![]() Γ±Κ≈«ρΓΔΥΡΗωΈόΚ≈«ρΘ§
Γ±Κ≈«ρΓΔΥΡΗωΈόΚ≈«ρΘ§![]() œδΡΎ”–ΈεΗωΓΑ
œδΡΎ”–ΈεΗωΓΑ![]() Γ±Κ≈«ρΓΔΈεΗωΓΑ
Γ±Κ≈«ρΓΔΈεΗωΓΑ![]() Γ±Κ≈«ρΘ§ΟΩ¥ΈΟΰΫ±ΚσΖ≈ΜΊΘ§œϊΖ―Εν¬ζ
Γ±Κ≈«ρΘ§ΟΩ¥ΈΟΰΫ±ΚσΖ≈ΜΊΘ§œϊΖ―Εν¬ζ![]() ‘Σ”–“Μ¥Έ
‘Σ”–“Μ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘ§œϊΖ―Εν¬ζ
œδΡΎΟΰΫ±ΜζΜαΘ§œϊΖ―Εν¬ζ![]() ‘Σ”–“Μ¥Έ
‘Σ”–“Μ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘ§ΟΰΒΟ”– ΐΉ÷ΒΡ«ρ‘ρ÷–Ϋ±Θ§ΓΑ
œδΡΎΟΰΫ±ΜζΜαΘ§ΟΰΒΟ”– ΐΉ÷ΒΡ«ρ‘ρ÷–Ϋ±Θ§ΓΑ![]() Γ±Κ≈«ρΫ±
Γ±Κ≈«ρΫ±![]() ‘ΣΓΔΓΑ
‘ΣΓΔΓΑ![]() Γ±Κ≈«ρΫ±
Γ±Κ≈«ρΫ±![]() ‘ΣΓΔΓΑ
‘ΣΓΔΓΑ![]() Γ±Κ≈«ρΫ±
Γ±Κ≈«ρΫ±![]() ‘ΣΘ§ΟΰΒΟΈόΚ≈«ρ‘ρΟΜ”–Ϋ±Ϋπ.
‘ΣΘ§ΟΰΒΟΈόΚ≈«ρ‘ρΟΜ”–Ϋ±Ϋπ.
Θ®ΔώΘ©Ψ≠Ά≥ΦΤΘ§œϊΖ―Εν![]() Ζΰ¥”’ΐΧ§Ζ÷≤Φ
Ζΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§Ρ≥Χλ”–
Θ§Ρ≥Χλ”–![]() ΈΣΙΥΩΆΘ§«κΙάΦΤœϊΖ―Εν
ΈΣΙΥΩΆΘ§«κΙάΦΤœϊΖ―Εν![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©‘Ύ«χΦδ
Θ®ΒΞΈΜΘΚ‘ΣΘ©‘Ύ«χΦδ![]() ΡΎ≤Δ÷–Ϋ±ΒΡ»Υ ΐΘΜ
ΡΎ≤Δ÷–Ϋ±ΒΡ»Υ ΐΘΜ
Θ®ΔρΘ©Ρ≥»ΐΈΜΙΥΩΆΗς”–“Μ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘ§«σΤδ÷–÷–Ϋ±»Υ ΐ
œδΡΎΟΰΫ±ΜζΜαΘ§«σΤδ÷–÷–Ϋ±»Υ ΐ![]() ΒΡΖ÷≤ΦΝ–ΘΜ
ΒΡΖ÷≤ΦΝ–ΘΜ
Θ®ΔσΘ©Ρ≥ΙΥΩΆœϊΖ―ΕνΈΣ![]() ‘ΣΘ§”–ΝΫ÷÷ΟΰΫ±ΖΫΖ®Θ§ΖΫΖ®“ΜΘΚ»ΐ¥Έ
‘ΣΘ§”–ΝΫ÷÷ΟΰΫ±ΖΫΖ®Θ§ΖΫΖ®“ΜΘΚ»ΐ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘΜΖΫΖ®ΕΰΘΚ“Μ¥Έ
œδΡΎΟΰΫ±ΜζΜαΘΜΖΫΖ®ΕΰΘΚ“Μ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘ§«κΈ ΘΚ’βΈΜΙΥΩΆ―ΓΡΡ“Μ÷÷ΖΫΖ®ΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΫœ¥σ.
œδΡΎΟΰΫ±ΜζΜαΘ§«κΈ ΘΚ’βΈΜΙΥΩΆ―ΓΡΡ“Μ÷÷ΖΫΖ®ΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΫœ¥σ.
ΗΫΘΚ»τ![]() Θ§‘ρ
Θ§‘ρ![]()
ΓΨ¥πΑΗΓΩ(Δώ)286;(Δρ)¥πΑΗΦϊΫβΈωΘΜ(Δσ)’βΈΜΙΥΩΆ―ΓΖΫΖ®ΕΰΥυΒΟΒΡΤΎΆϊ÷ΒΫœ¥σ.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®ΔώΘ©“άΧβ“βΒΟΠΧ=150Θ§Π“2=625Θ§ΒΟΠ“=25Θ§100=ΠΧ©¹2Π“Θ§œϊΖ―ΕνX‘Ύ«χΦδΘ®100Θ§150]ΡΎΒΡΙΥΩΆ”–“Μ¥ΈAœδΡΎΟΰΫ±ΜζΜαΘ§÷–Ϋ±¬ ΈΣ0.6Θ§»Υ ΐ‘ΦΈΣ1000ΓΝPΘ®ΠΧ©¹2Π“ΘΦXΓήΠΧΘ©Θ§Ω…ΒΟΤδ÷–÷–Ϋ±ΒΡ»Υ ΐΘ°
Θ®ΔρΘ©»ΐΈΜΙΥΩΆΟΩ»Υ“Μ¥ΈAœδΡΎΟΰΫ±÷–Ϋ±¬ ΕΦΈΣ0.6Θ§»ΐ»Υ÷–÷–Ϋ±»Υ ΐΠΈΖΰ¥”ΕΰœνΖ÷≤ΦBΘ®3Θ§0.6Θ©Θ§![]() Θ§Θ®k=0Θ§1Θ§2Θ§3Θ©Θ§Φ¥Ω…ΒΟ≥ωΘ°
Θ§Θ®k=0Θ§1Θ§2Θ§3Θ©Θ§Φ¥Ω…ΒΟ≥ωΘ°
Θ®ΔσΘ©άϊ”Ο ΐ―ßΤΎΆϊΒΡΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΘ°
‘ΧβΫβΈωΘΚ
Θ®ΔώΘ©“άΧβ“βΒΟ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
œϊΖ―Εν![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() ΡΎΒΡΙΥΩΆ”–“Μ¥Έ
ΡΎΒΡΙΥΩΆ”–“Μ¥Έ![]() œδΡΎΟΰΫ±ΜζΜαΘ§÷–Ϋ±¬ ΈΣ
œδΡΎΟΰΫ±ΜζΜαΘ§÷–Ϋ±¬ ΈΣ![]() Θ§
Θ§
»Υ ΐ‘ΦΈΣ![]() »ΥΘ§
»ΥΘ§
Τδ÷–÷–Ϋ±ΒΡ»Υ ΐ‘ΦΈΣ![]() »ΥΘ§
»ΥΘ§
Θ®ΔρΘ©»ΐΈΜΙΥΩΆΟΩ»Υ“Μ¥Έ![]() œδΡΎΟΰΫ±÷–Ϋ±¬ ΕΦΈΣ
œδΡΎΟΰΫ±÷–Ϋ±¬ ΕΦΈΣ![]() Θ§
Θ§
»ΐ»Υ÷–÷–Ϋ±»Υ ΐ![]() Ζΰ¥”ΕΰœνΖ÷≤Φ
Ζΰ¥”ΕΰœνΖ÷≤Φ![]()
Ι ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
 Θ®ΔσΘ©
Θ®ΔσΘ©![]() œδΟΰ“Μ¥ΈΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ
œδΟΰ“Μ¥ΈΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ![]() Θ§
Θ§
![]() œκΟΰ“Μ¥ΈΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ
œκΟΰ“Μ¥ΈΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ![]() Θ§
Θ§
ΖΫΖ®“ΜΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ![]() Θ§ΖΫΖ®ΕΰΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ
Θ§ΖΫΖ®ΕΰΥυΒΟΫ±ΫπΒΡΤΎΆϊ÷ΒΈΣ![]() Θ§
Θ§
Υυ“‘’βΈΜΙΥΩΆ―ΓΖΫΖ®ΕΰΥυΒΟΒΡΤΎΆϊ÷ΒΫœ¥σ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΤΫΟφ”κΩ’ΦδΥΡ±Ώ–Έ![]() ΒΡΕ‘Ϋ«œΏ
ΒΡΕ‘Ϋ«œΏ![]() Θ§
Θ§![]() ΕΦΤΫ––Θ§«“ΫΜΩ’ΦδΥΡ±Ώ–ΈΒΡ±Ώ
ΕΦΤΫ––Θ§«“ΫΜΩ’ΦδΥΡ±Ώ–ΈΒΡ±Ώ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±π”Ύ
Ζ÷±π”Ύ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
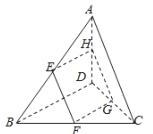
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–Έ![]() ΈΣΤΫ––ΥΡ±Ώ–ΈΘΜ
ΈΣΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»τ![]() «±Ώ
«±Ώ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§![]() Θ§
Θ§![]() Θ§“λΟφ÷±œΏ
Θ§“λΟφ÷±œΏ![]() ”κ
”κ![]() Υυ≥…ΒΡΫ«ΈΣ60ΓψΘ§«σœΏΕΈ
Υυ≥…ΒΡΫ«ΈΣ60ΓψΘ§«σœΏΕΈ![]() ΒΡ≥ΛΕ».
ΒΡ≥ΛΕ».
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©Β±![]() ±,
±,![]() Κψ≥…ΝΔ,«σ Β ΐ
Κψ≥…ΝΔ,«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß;
ΒΡ»Γ÷ΒΖΕΈß;
Θ®2Θ© «ΖώΆ§ ±¥φ‘Ύ Β ΐ![]() ΚΆ’ΐ’ϊ ΐ
ΚΆ’ΐ’ϊ ΐ![]() , ΙΒΟΚ· ΐ
, ΙΒΟΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œ«Γ”–2019ΗωΝψΒψ
…œ«Γ”–2019ΗωΝψΒψ![]() »τ¥φ‘Ύ,«κ«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡ
»τ¥φ‘Ύ,«κ«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡ![]() ΚΆ
ΚΆ![]() ΒΡ÷Β;»τ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”….
ΒΡ÷Β;»τ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®2Θ©»τΙΊ”Ύ![]() ΒΡΖΫ≥Χ
ΒΡΖΫ≥Χ![]() ”–»ΐΗω≤ΜΆ§ΒΡ ΒΗυΘ§«σ Β ΐ
”–»ΐΗω≤ΜΆ§ΒΡ ΒΗυΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©“―÷ΣΨΊ–ΈΒΡΟφΜΐΈΣ100Θ§‘ρ’βΗωΨΊ–ΈΒΡ≥ΛΓΔΩμΗςΈΣΕύ…Ό ±Θ§ΨΊ–ΈΒΡ÷ή≥ΛΉνΕΧΘΩΉνΕΧ÷ή≥Λ «Εύ…ΌΘΩ
Θ®2Θ©“―÷ΣΨΊ–ΈΒΡ÷ή≥ΛΈΣ36Θ§‘ρ’βΗωΨΊ–ΈΒΡ≥ΛΓΔΩμΗςΈΣΕύ…Ό ±Θ§ΥϋΒΡΟφΜΐΉν¥σΘΩΉν¥σΟφΜΐ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§«ζœΏ![]() ”…«ζœΏ
”…«ζœΏ![]() ΚΆ«ζœΏ
ΚΆ«ζœΏ![]() Ήι≥…Θ§Τδ÷–Βψ
Ήι≥…Θ§Τδ÷–Βψ![]() ΈΣ«ζœΏ
ΈΣ«ζœΏ![]() Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§Βψ
Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§Βψ![]() ΈΣ«ζœΏ
ΈΣ«ζœΏ![]() Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψ.
Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψ.
Θ®ΔώΘ©»τ![]() Θ§«σ«ζœΏ
Θ§«σ«ζœΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»γΆΦΘ§Ής÷±œΏ![]() ΤΫ––”Ύ«ζœΏ
ΤΫ––”Ύ«ζœΏ![]() ΒΡΫΞΫϋœΏΘ§ΫΜ«ζœΏ”ΎΒψ
ΒΡΫΞΫϋœΏΘ§ΫΜ«ζœΏ”ΎΒψ![]() Θ§«σ÷ΛΘΚœ“
Θ§«σ÷ΛΘΚœ“![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() ±Ί‘Ύ«ζœΏ
±Ί‘Ύ«ζœΏ![]() ΒΡΝμ“ΜΧθΫΞΫχœΏ…œΘΜ
ΒΡΝμ“ΜΧθΫΞΫχœΏ…œΘΜ
Θ®ΔσΘ©Ε‘”ΎΘ®ΔώΘ©÷–ΒΡ«ζœΏ![]() ,»τ÷±œΏ
,»τ÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() ΫΜ«ζœΏ
ΫΜ«ζœΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ΟφΜΐ÷°ΚΆΒΡΉν¥σ÷Β.
ΟφΜΐ÷°ΚΆΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
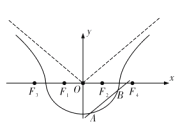
ΓΨΧβΡΩΓΩ…ηΥΪ«ζœΏ![]() ΒΡΉσΘ§”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§ΙΐF1ΒΡ÷±œΏlΫΜΥΪ«ζœΏΉσ÷ß”ΎAΘ§BΝΫΒψΘ§‘ρ|BF2|ΘΪ|AF2|ΒΡΉν–Γ÷ΒΈΣ(ΓΓΓΓ)
ΒΡΉσΘ§”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§ΙΐF1ΒΡ÷±œΏlΫΜΥΪ«ζœΏΉσ÷ß”ΎAΘ§BΝΫΒψΘ§‘ρ|BF2|ΘΪ|AF2|ΒΡΉν–Γ÷ΒΈΣ(ΓΓΓΓ)
A. ![]() B. 11
B. 11
C. 12 D. 16
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©…η![]() Θ§«σΚ· ΐ
Θ§«σΚ· ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©“―÷Σ![]() Θ§«σΚ· ΐ
Θ§«σΚ· ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®4Θ©…η![]() Θ§«“
Θ§«“![]() Θ§«σ
Θ§«σ![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊΓςA1B1C1ΒΡ»ΐΗωΡΎΫ«ΒΡ”ύœ“÷ΒΖ÷±πΒ»”ΎΓςA2B2C2ΒΡ»ΐΗωΡΎΫ«ΒΡ’ΐœ“÷ΒΘ§‘ρΘ® Θ©
A.ΓςA1B1C1ΚΆΓςA2B2C2ΕΦ «»ώΫ«»ΐΫ«–Έ
B.ΓςA1B1C1ΚΆΓςA2B2C2ΕΦ «ΕέΫ«»ΐΫ«–Έ
C.ΓςA1B1C1 «ΕέΫ«»ΐΫ«–ΈΘ§ΓςA2B2C2 «»ώΫ«»ΐΫ«–Έ
D.ΓςA1B1C1 «»ώΫ«»ΐΫ«–ΈΘ§ΓςA2B2C2 «ΕέΫ«»ΐΫ«–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com