
【题目】如图,一平面与空间四边形![]() 的对角线
的对角线![]() ,
,![]() 都平行,且交空间四边形的边
都平行,且交空间四边形的边![]() ,
,![]() ,
,![]() ,
,![]() 分别于
分别于![]() ,
,![]() ,
,![]() ,
,![]() .
.
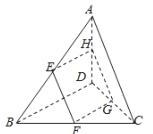
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为60°,求线段
所成的角为60°,求线段![]() 的长度.
的长度.
科目:高中数学 来源: 题型:
【题目】“人机大战,柯洁哭了,机器赢了”,2017年5月27日,![]() 岁的世界围棋第一人柯洁
岁的世界围棋第一人柯洁![]() 不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的
不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的![]() 男性中,有
男性中,有![]() 人持反对意见,
人持反对意见,![]() 名女性中,有
名女性中,有![]() 人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.分层抽样B.回归分析C.独立性检验D.频率分布直方图
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中(底面△ABC为正三角形),A1A⊥平面ABC,AB=AC=2,![]() ,D是BC边的中点.
,D是BC边的中点.
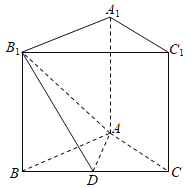
(1)证明:平面ADB1⊥平面BB1C1C.
(2)求点B到平面ADB1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为2的正方形,SA=SB=SC=SD![]() ,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
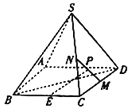
(1)证明:EP∥平面SBD;
(2)求四棱锥S﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球、两个“
”号球、两个“![]() ”号球、三个“
”号球、三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球、五个“
”号球、五个“![]() ”号球,每次摸奖后放回,消费额满
”号球,每次摸奖后放回,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金.
元,摸得无号球则没有奖金.
(Ⅰ)经统计,消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 为顾客,请估计消费额
为顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数;
内并中奖的人数;
(Ⅱ)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列;
的分布列;
(Ⅲ)某顾客消费额为![]() 元,有两种摸奖方法,方法一:三次
元,有两种摸奖方法,方法一:三次![]() 箱内摸奖机会;方法二:一次
箱内摸奖机会;方法二:一次![]() 箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
附:若![]() ,则
,则![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com