
 ����ż����{2n}�е���������С�´���С�Ҵ�ԭ���ų���ͼ�������Ρ���ʾ����������aij��i��j��N*����λ����������������д�����������i�У�������������j������
����ż����{2n}�е���������С�´���С�Ҵ�ԭ���ų���ͼ�������Ρ���ʾ����������aij��i��j��N*����λ����������������д�����������i�У�������������j������| 52n |
| 5n-1 |
| 4 |
| 3 |
| m(m-1) |
| 2 |
| 4 |
| 3 |
| m(m-1) |
| 2 |
| |||
| 5n |
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
| ||
| 2 |
| ||
| 2 |
| n |
| 5n |
| 1 |
| 5 |
| 2 |
| 52 |
| 3 |
| 53 |
| n |
| 5n |
| 1 |
| 5 |
| 1 |
| 52 |
| 2 |
| 53 |
| n |
| 5n+1 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 53 |
| 1 |
| 5n |
| 1 |
| 5n+1 |
| 5 |
| 16 |
| 4n+5 |
| 16��5n |
| 52n |
| 5n-1 |
| 52n |
| 5n-1 |
| n |
| 5n |
| n5n |
| 5n-1 |
| 51 |
| 5n-1 |
| 52 |
| 5n-1 |
| 5n |
| 5n-1 |
| 4 |
| 3 |
| 51 |
| 5n-1 |
| 52 |
| 5n-1 |
| 5n |
| 5n-1 |
| 4 |
| 3 |
| 5-1 |
| 5 |
| 52-1 |
| 52 |
| 5n-1 |
| 5n |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5n |
| 3 |
| 4 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5n |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5n |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5k+1 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5k+1 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5k+1 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5k+1 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5k |
| 1 |
| 5k+1 |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5n |
| 1 |
| 5 |
| 1 |
| 52 |
| 1 |
| 5n |
| ||||
1-
|
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5n |
| 3 |
| 4 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2009-2010ѧ�����ʡТ�и��и������ϣ�9���ۺϲ�����ѧ�Ծ�2�����ƣ��������棩 ���ͣ������
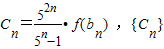 ��ǰn��֮��ΪTn��n��N*������֤��
��ǰn��֮��ΪTn��n��N*������֤��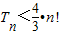 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
2
4 6
8 10 12
14 16 18 20
22 24 26 28 30
��
(1)���������������д�����������n�и�����֮��Ϊbn,������{bn}��ͨ�ʽ.
(2)��cn-1=![]() (n��2),������{cn}��ǰn���Sn.
(n��2),������{cn}��ǰn���Sn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
2
4 6
8 10 12
14 16 18 20
22 24 26 28 30
��
(1)���������������д�����������n�и�����֮��Ϊbn,������{bn}��ͨ�ʽ;
(2)��cn-1=![]() (n��2),����{cn}��ǰn���ΪSn,��
(n��2),����{cn}��ǰn���ΪSn,��![]() Sn��ֵ.
Sn��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com