
分析 (1)由题意可得2c=6,e=3,由离心率公式和a,b,c的关系,可得a,b,进而得到所求双曲线的方程;
(2)设抛物线的方程为y2=mx,求得焦点和准线方程,由题意可得$\frac{|m|}{2}$=1,即可得到所求抛物线的方程.
解答 解:(1)由题意可得2c=6,e=3,
即有c=3,$\frac{c}{a}$=3,a2+b2=c2,
解得a=1,b=2$\sqrt{2}$,
则所求双曲线的方程为x2-$\frac{{y}^{2}}{8}$=1或y2-$\frac{{x}^{2}}{8}$=1;
(2)设抛物线的方程为y2=mx,
焦点为($\frac{m}{4}$,0),准线为x=-$\frac{m}{4}$,
由题意可得$\frac{|m|}{2}$=1,
即有m=±2,
则所求抛物线的方程为y2=2x或y2=-2x.
点评 本题考查双曲线和抛物线的方程的求法,考查待定系数法的运用,考查运算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
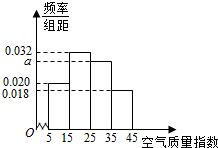 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin15°cos15° | B. | cos2$\frac{π}{12}$-sin2$\frac{π}{12}$ | ||
| C. | $\frac{tan22.5°}{1-ta{n}^{2}22.5°}$ | D. | $\frac{1+tan15°}{1-tan15°}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱柱被平面分成的两部分可以都是棱柱 | |
| B. | 底面是矩形的平行六面体是长方体 | |
| C. | 棱柱的底面一定是平行四边形 | |
| D. | 棱锥的底面一定是三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 有60m长的钢材,要制作如图所示的窗框:
有60m长的钢材,要制作如图所示的窗框:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com