
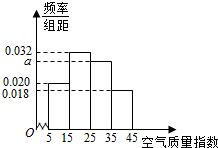
 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.分析 (1)由频率分布直方图中小矩形面积之和为1,由此能求出a.
(2)由已知得X的取值为0,1,2,3,且X~B(3,$\frac{1}{5}$),由此能求出X的分布列和EX.
解答 解:(1)由频率分布直方图中小矩形面积之和为1,
得:(0.02+0.032+a+0.018)×10=1,
解得a=0.03.
(2)利用样本估计总体,该年度空所质量指数在(5,15]内为“特优等级”,
且指数达到“特优等级”的概率为0.2,
则X的取值为0,1,2,3,且X~B(3,$\frac{1}{5}$),
P(X=0)=${C}_{3}^{0}(\frac{4}{5})^{3}$=$\frac{64}{125}$,
P(X=1)=${C}_{3}^{1}(\frac{1}{5})(\frac{4}{5})^{2}$=$\frac{48}{125}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{5})^{2}(\frac{4}{5})$=$\frac{12}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{1}{5})^{3}=\frac{1}{125}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
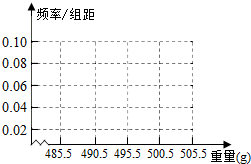 某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:
某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | |
| [490.5,495.5) | 0.20 | |
| [495.5,500.5) | 50 | |
| [500.5,505.5] | ||
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
| 价格(万元) | 25 | 23.5 | 22 | 20.5 |
| 销售量(辆) | 30 | 33 | 36 | 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com