
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
| 价格(万元) | 25 | 23.5 | 22 | 20.5 |
| 销售量(辆) | 30 | 33 | 36 | 39 |
分析 (1)100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访,A、B、C型汽车各2,4,4辆.从参加问卷到访的10辆汽车中随机抽取两辆,有${C}_{10}^{2}$=45种方法,即可求这两辆汽车来自同一类型的概率;
(2)ξ的取值为0,200,400,600,求出相应的概率,即可求ξ的分布列及数学期望;
(3)求出b,即可预测月销售量.
解答 解:(1)100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访,A、B、C型汽车各2,4,4辆.
从参加问卷到访的10辆汽车中随机抽取两辆,有${C}_{10}^{2}$=45种方法,这两辆汽车来自同一类型的概率为$\frac{{C}_{2}^{2}+2{C}_{4}^{2}}{45}$=$\frac{13}{45}$;
(2)ξ的取值为0,200,400,600,
P(ξ=0)=0.8×0.6×0.6=0.288,P(ξ=200)=0.2×0.6×0.6+0.8×0.4×0.6+0.8×0.6×0.4=0.456,
P(ξ=400)=0.2×0.4×0.6+0.2×0.6×0.4+0.8×0.4×0.4=0.224,
P(ξ=600)=0.2×0.4×0.4=0.032,
∴ξ的分布列
| ξ | 0 | 200 | 400 | 600 |
| P | 0.288 | 0.456 | 0.224 | 0.032 |
点评 本题考查概率的计算,考查分布列及数学期望,考查线性回归方程,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.432 | C. | 0.45 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
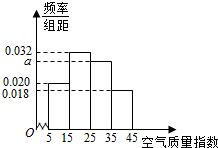 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱柱被平面分成的两部分可以都是棱柱 | |
| B. | 底面是矩形的平行六面体是长方体 | |
| C. | 棱柱的底面一定是平行四边形 | |
| D. | 棱锥的底面一定是三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
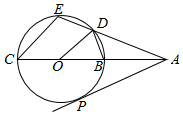 如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com