
【题目】【2018届天津市耀华中学高三上学期第三次月考】已知椭圆![]() 的一个焦点在直线
的一个焦点在直线![]() 上,且离心率
上,且离心率![]() .
.
(1)求该椭圆的方程;
(2)若![]() 与
与![]() 是该椭圆上不同的两点,且线段
是该椭圆上不同的两点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,试证:
上,试证: ![]() 轴上存在定点
轴上存在定点![]() ,对于所有满足条件的
,对于所有满足条件的![]() 与
与![]() ,恒有
,恒有![]() ;
;
(3)在(2)的条件下, ![]() 能否为等腰直角三角形?并证明你的结论.
能否为等腰直角三角形?并证明你的结论.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析: ![]() 利用椭圆的性质,离心率计算公式
利用椭圆的性质,离心率计算公式![]() 及
及![]() 即可求出;
即可求出;
⑵分直线![]() 的斜率存在与不存在两种情况:
的斜率存在与不存在两种情况: ![]() 斜率存在时,设出其方程,与椭圆方程联立得到关于斜率的方程式,从而得到
斜率存在时,设出其方程,与椭圆方程联立得到关于斜率的方程式,从而得到![]() 坐标间的关系式。假设
坐标间的关系式。假设![]() 轴上存在定点
轴上存在定点![]() ,对于所有满足条件的
,对于所有满足条件的![]() ,恒有
,恒有![]() ,得到点
,得到点![]() 的坐标,即证命题存在;当直线
的坐标,即证命题存在;当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() 成立,命题得证;
成立,命题得证;
⑶分类讨论,利用等腰直角三角形的性质和两点间的距离关系及其根与系数的关系即可得到满足条件的直线斜率![]() 存在即可;
存在即可;
解析:(1)∵椭圆![]() 的一个焦点在直线
的一个焦点在直线![]() 上,∴
上,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴该椭圆的方程为![]() .
.
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
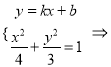
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
∵弦![]() 的中点
的中点![]() 在直线
在直线![]() 上,∴
上,∴![]()
![]() ,
,
∴![]()
![]() ,∴
,∴![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,
,
假设在![]() 轴上存在定点
轴上存在定点![]() ,
, ![]()
![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]()
![]() ,即
,即![]() ,
,
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 垂直于
垂直于![]() 轴,此时
轴,此时![]() 显然成立,综上,
显然成立,综上, ![]() 轴上存在定点
轴上存在定点![]() .
.
(3)假设![]() 能为等腰直角三角形,则
能为等腰直角三角形,则![]() ,
,
∴![]() ,
,
![]() ,
,
![]()
![]() ,
,
又![]() ,
,
∴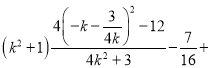
![]() ,
,
![]()
![]() ,符合(*),
,符合(*),
∴在(2)的条件下, ![]() 能为等腰直角三角形.
能为等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
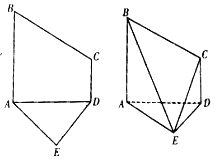
【题目】已知五边形![]() 是由直角梯形
是由直角梯形![]() 和等腰直角三角形
和等腰直角三角形![]() 构成,如图所示,
构成,如图所示, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,将五边形
,将五边形![]() 沿着
沿着![]() 折起,且使平面
折起,且使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() 为
为![]() 中点,边
中点,边![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
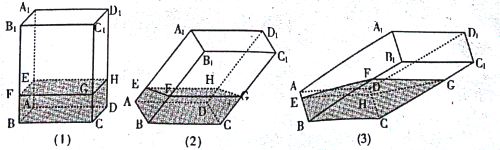
【题目】如图,透明塑料制成的长方体ABCD﹣A1B1C1D1内灌进一些水,固定容器底面一边BC于水平地面上,再将容器倾斜,随着倾斜度不同,有下面五个命题:
①有水的部分始终呈棱柱形;
②没有水的部分始终呈棱柱形;
③水面EFGH所在四边形的面积为定值;
④棱A1D1始终与水面所在平面平行;
⑤当容器倾斜如图(3)所示时,BEBF是定值.
其中所有正确命题的序号是 ____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() 平面
平面![]() ,垂足为H,给出下面结论:
,垂足为H,给出下面结论:
①直线![]() 与该正方体各棱所成角相等;
与该正方体各棱所成角相等;
②直线![]() 与该正方体各面所成角相等;
与该正方体各面所成角相等;
③过直线![]() 的平面截该正方体所得截面为平行四边形;
的平面截该正方体所得截面为平行四边形;
④垂直于直线![]() 的平面截该正方体,所得截面可能为五边形,
的平面截该正方体,所得截面可能为五边形,
其中正确结论的序号为( )
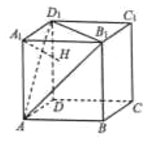
A. ①③ B. ②④ C. ①②④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.


表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少千册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com