
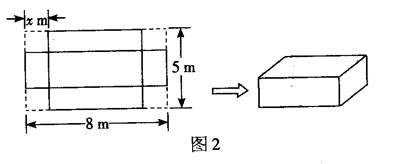
. (本小题满分12分)如图2所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?
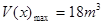 ,此时
,此时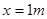 。
。
【解析】此题主要考查用代数式表示正方形、矩形的面积和体积、考查函数求最值在实际问题中的应用,其中涉及到由导函数分类讨论单调性的思想,在高考中属于重点考点,同学们需要理解并记忆.
首先分析题目求长为8m,宽为5m的长方形铁皮做一个无盖长方体,当长方体的高为多少时,容积最大.故可根据边长为xm的正方形,求出长方体的体积f(x)关于x的方程,然后求出导函数,分析单调性即可求得最值.

解:无盖长方体的底面长为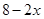 ,宽为
,宽为 ,高为
,高为
其体积  ……(4分)
……(4分)
其中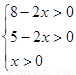 ,则0
,则0 ……………(5分)
……………(5分)
令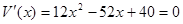
得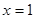 或
或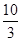 (舍)…………………………………………………(8分)
(舍)…………………………………………………(8分)
当 时,
时,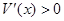 ;当
;当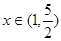 时,
时,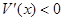 ………(10分)
………(10分)
因此,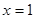 是V(x)的极大值点,也是
是V(x)的极大值点,也是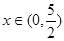 上的最大值点
上的最大值点
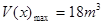 ,此时
,此时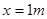 ……………………………………(12分)
……………………………………(12分)


科目:高中数学 来源: 题型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知关于![]() 的一元二次函数
的一元二次函数![]() (Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率;(Ⅱ)设点(
上是增函数的概率;(Ⅱ)设点(![]() ,
,![]() )是区域
)是区域 内的随机点,求函数
内的随机点,求函数![]() 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分) 一几何体![]() 的三视图如图所示,
的三视图如图所示,![]() ,A1A=
,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() 在线段
在线段![]() 上且
上且![]() =
=![]() .
.
(I)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com