
【题目】如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点. 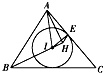
(1)求证A,I,H,E四点共圆;
(2)若∠C=50°,求∠IEH的度数.
【答案】
(1)证明:由圆I与AC相切于点E得IE⊥AC,结合HI⊥AH,得∠AEI=∠AHI=90°,所以A,I,H,E四点共圆.
(2)解:由(1)知A,I,H,E四点共圆,在此圆中∠IEH与∠IAH对同弧,
∴∠IEH=∠HAI.
∵锐角△ABC的内心为I,
∴AI、BI分别是∠BAC、∠ABC的平分线,
可得∠HIA=∠ABI+∠BAI= ![]() ∠ABC+
∠ABC+ ![]() ∠BAC=
∠BAC= ![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)= ![]() (180°﹣∠C)=90°﹣
(180°﹣∠C)=90°﹣ ![]() ∠C,
∠C,
结合IH⊥AH,得∠HAI=90°﹣∠HIA=90°﹣(90°﹣ ![]() ∠C)=
∠C)= ![]() ∠C,所以∠IEH=
∠C,所以∠IEH= ![]() ∠C.
∠C.
由∠C=50°得∠IEH=25°
【解析】(1)由于⊙I切AC于点E,可得IE⊥AC,又AH⊥IH,可得A、I、H、E四点共圆;(2)在此圆中∠IEH与∠IAH对同弧.再利用三角形内角平分线的性质和三角形的内角和定理即可得出.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sinxcosx﹣sin2x,把f(x)的图象向右平移
sinxcosx﹣sin2x,把f(x)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+
个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α﹣x)=g(α+x)成立,则g(α+ ![]() )+g(
)+g( ![]() )=( )
)=( )
A.4
B.3
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() .有序数组
.有序数组 ![]() 经m次变换后得到数组
经m次变换后得到数组 ![]() ,其中
,其中 ![]() ,
, ![]() (
( ![]() 1,2,
1,2, ![]() ,n),
,n), ![]() ,
, ![]()
![]() .
.
例如:有序数组 ![]() 经1次变换后得到数组
经1次变换后得到数组 ![]() ,即
,即 ![]() ;经第2次变换后得到数组
;经第2次变换后得到数组 ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)求证: ![]() ,其中
,其中 ![]() 1,2,
1,2, ![]() ,n.(注:当
,n.(注:当 ![]() 时,
时, ![]() ,
, ![]() 1,2,
1,2, ![]() ,n,则
,n,则 ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面ABCD是菱形,∠ABC=60°,AB=PC=2, ![]() .
. 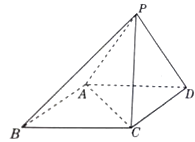
(1)求证:平面PAD⊥平面ABCD;
(2)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数a,b,定义min{a,b}= ![]() ,定义在R上的偶函数f (x)满足f (x+4)=f(x),且当0≤x≤2时,f (x)=min{2x﹣1,2﹣x},若方程f (x)﹣mx=0恰有两个根,则m的取值范围是( )
,定义在R上的偶函数f (x)满足f (x+4)=f(x),且当0≤x≤2时,f (x)=min{2x﹣1,2﹣x},若方程f (x)﹣mx=0恰有两个根,则m的取值范围是( )
A.{﹣1,1}∪(﹣ln2,- ![]() )∪(
)∪( ![]() ,ln2)
,ln2)
B.[﹣1,- ![]() )∪
)∪ ![]()
C.{﹣1,1}∪(﹣ln2,- ![]() )∪(
)∪( ![]() ,ln2)
,ln2)
D.(- ![]() ,-
,- ![]() )∪(
)∪( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣6x2+9x,g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
A.(1, ![]() ]??
]??
B.[9,+∞)??
C.(1, ![]() ]∪[9,+∞)??
]∪[9,+∞)??
D.[ ![]() ,
, ![]() ]∪[9,+∞)
]∪[9,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是椭圆C: ![]() =1(a>b>0)的两个焦点,P(1,
=1(a>b>0)的两个焦点,P(1, ![]() )是椭圆上一点,且
)是椭圆上一点,且 ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差数列.
|PF2|成等差数列.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F2 , 且与椭圆C交于A、B两点,试问x轴上是否存在定点Q,使得 ![]() =﹣
=﹣ ![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com