设函数满足f(x)+f(-x)=0,且f(x)在[-2,2]是减函数,f(2)=-1,若函数f(x)≤t2+2ta+1对所有x∈[-2,2],a∈[-1,1]时,则t的取值范围是________.
解:因为f(x)+f(-x)=0,所以f(x)为奇函数,
∵f(2)=-1,∴f(-2)=1.
∴f(x)的取值范围为[-1,1].
∵函数f(x)≤t
2+2ta+1对所有x∈[-2,2],a∈[-1,1]
∴t
2+2ta+1对要大于等于f(x) 的最大值即为t
2+2ta+1≥1
∴t
2+2ta≥0
令g(a)=2ta+t
2,则
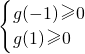
,即

∴t≥2或t≤-2
∴t的取值范围为(-∞,-2)∪(2,∞)
故答案为:(-∞,-2)∪(2,∞)
分析:根据f(x)+f(-x)=0,f(2)=-1,确定f(x)的取值范围;函数f(x)≤t
2+2ta+1对所有x∈[-2,2],a∈[-1,1]等价于t
2+2ta+1≥1,即t
2+2ta≥0,构建一次函数g(a)=2ta+t
2,从而可建立不等式,进而可求t的取值范围.
点评:本题考查函数的奇偶性、单调性,考查恒成立问题,解题的关键是转化为t
2+2ta+1对要大于等于f(x) 的最大值,属于中档题.

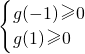 ,即
,即

