
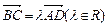 ,
,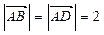 ,
,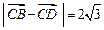 .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求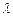 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求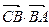 .
.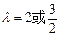 (Ⅱ)-3
(Ⅱ)-3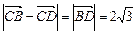 ,在
,在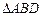 中,由余弦定理,得
中,由余弦定理,得 ,∴
,∴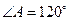 ,(2分)由
,(2分)由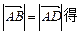 ,
,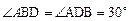 , 由
, 由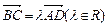 得,
得,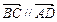 ,
,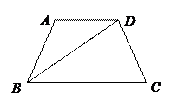
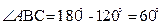 ,从而
,从而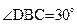 (4分)
(4分)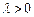 ,∴
,∴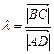 , (5分)
, (5分)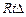 ,∴
,∴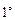 当
当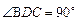 时,则
时,则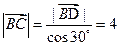 ,由
,由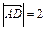 ,
,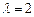 ;
; 当
当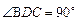 时,则
时,则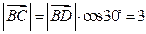 ,由
,由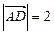 ,∴
,∴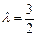 ;
;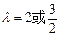 .(7分)
.(7分)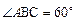 ,∴向量
,∴向量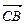 与
与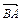 的夹角为
的夹角为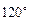 ,
, 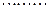 (9分)
(9分)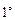 当
当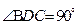 时,
时, ,
,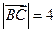 ,
,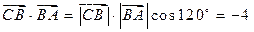 .
.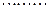 (10分)
(10分)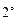 当
当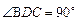 时,
时, ,
,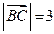 ,
,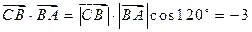 .
. (12分)
(12分)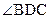 是直角三形”来解,忽略对
是直角三形”来解,忽略对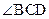 为直角的情况的讨论;(2)在计算
为直角的情况的讨论;(2)在计算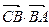 时,将
时,将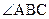 当作向量
当作向量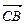 与
与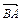 的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:不详 题型:单选题
| 3 |
| OA |
| OB |
A.-
| B.
| C.-
| D.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 7 |
| 3 |
| OM |
| OA |
| OB |
| OM |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 斜率为
斜率为 的直线
的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点,过
两点,过 且与
且与 垂直的直线
垂直的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于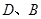 两点。
两点。 的取值范围;
的取值范围; 面积的最小值。
面积的最小值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com