
已知函数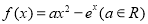
(Ⅰ)当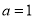 时,判断函数
时,判断函数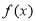 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若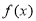 有两个极值点
有两个极值点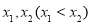 ,证明:
,证明: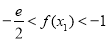 .
.
(Ⅰ)证明详见解析;(Ⅱ)证明详见解析.
【解析】
试题分析:(Ⅰ)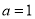 时,
时,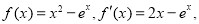 于是可利用导数的符号解决函数的单调性问题;(Ⅱ)因为
于是可利用导数的符号解决函数的单调性问题;(Ⅱ)因为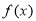 有两个极值点
有两个极值点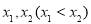 ,所以其导函数
,所以其导函数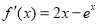 有两个零点,
有两个零点,
又因为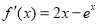 的导数为
的导数为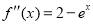 ,可结合
,可结合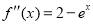 的性质确定的
的性质确定的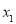 取值范围,写出函数
取值范围,写出函数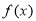 在处所取极值的表达式
在处所取极值的表达式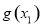 及定义域,同样利用导数研究
及定义域,同样利用导数研究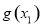 的单调性从而证明不等式
的单调性从而证明不等式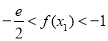 .
.
试题解析:(Ⅰ)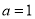 时,
时,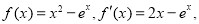
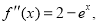 易知
易知
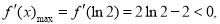 从而
从而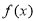 为单调减函数. 4分
为单调减函数. 4分
(Ⅱ)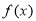 有两个极值点
有两个极值点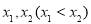 ,
,
即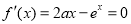 有两个实根
有两个实根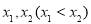 ,所以
,所以
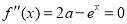 ,得
,得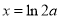 .
.
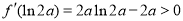 ,得
,得 . 6分
. 6分
又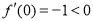 ,
,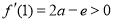
所以 8分
8分
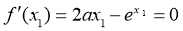 ,得
,得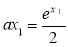
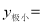
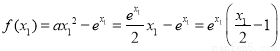
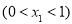 10分
10分
令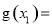

 ,
,
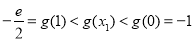 12分
12分
另【解析】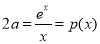 由两个实根,
由两个实根, ,
,
当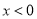 时,
时,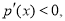 所以
所以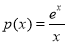 单调递减且
单调递减且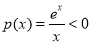 ,不能满足条件.
,不能满足条件.
当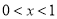 时,
时,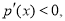 所以
所以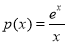 单调递减且
单调递减且
当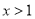 时,
时,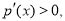 所以
所以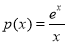 单调递增且
单调递增且 ,
,
故当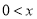 时,
时,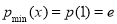 ,当
,当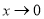 时
时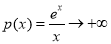 ,当
,当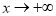 时②
时②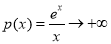 ,所以
,所以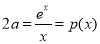 由两个实根需要
由两个实根需要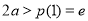 .即
.即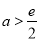
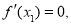 即
即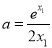 ,
,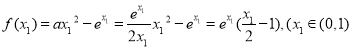 ,从而可以构造函数解决不等式的证明.
,从而可以构造函数解决不等式的证明.
考点:导数的运算以及应用导数研究函数的单调性、求函数的极值等问题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源:2014-2015学年山东省日照市高三12月校际联合检测理科数学试卷(解析版) 题型:选择题
已知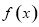 是定义在R上的奇函数,当
是定义在R上的奇函数,当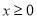 时,
时,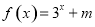 (m为常数),则
(m为常数),则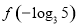 的值为( )
的值为( )
A.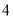 B.
B.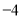 C.6 D.
C.6 D.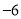
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图像,则只要将
的图像,则只要将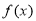 的图像( )
的图像( )

A.向右平移 个单位长度
个单位长度
B.向右平移 个单位长度
个单位长度
C.向左平移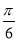 个单位长度
个单位长度
D.向左平移 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省等五校高三上学期第二次联考文科数学试卷(解析版) 题型:选择题
等差数列 的前
的前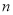 项和为
项和为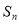 ,且
,且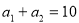 ,
,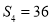 ,则过点
,则过点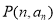 和
和 (
( )的直线的一个方向向量是
)的直线的一个方向向量是
A.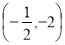 B.
B. C.
C.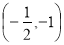 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为t件时,销售所得的收入为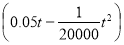 万元.
万元.
(1)该公司这种产品的年生产量为x件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x);
(2)当该公司的年产量为多少件时,当年所获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com