
如图,在四棱锥P ?ABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.
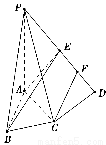
(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.
见解析
【解析】(1)因为PA⊥底面ABCD,所以PA⊥CD,(2分)
又AC⊥CD,且AC∩PA=A,所以CD⊥平面PAC,(4分)
又CD?平面PCD,所以平面PAC⊥平面PCD.(7分)
(2)取AE中点G,连接FG,BG.

因为F为ED的中点,所以FG∥AD且FG=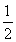 AD.(9分)
AD.(9分)
在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=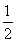 AD,所以BC=
AD,所以BC=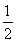 AD.(11分)
AD.(11分)
在△ABC中,AB=BC=AC,所以∠ACB=60°,
从而∠ACB=∠DAC,所以AD∥BC.
综上,FG∥BC,FG=BC,四边形FGBC为平行四边形,所以CF∥BG.(13分)
又BG?平面BAE,CF?平面BAE,所以CF∥平面BAE.(14分)


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
设函数f(x)=ax2+bx+c,且f(1)=-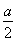 ,3a>2c>2b,求证:
,3a>2c>2b,求证:
(1)a>0,且-3<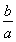 <-
<-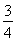 ;
;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则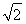 ≤|x1-x2|<
≤|x1-x2|<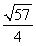 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
A.y=-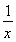 B.y=log2|x|
B.y=log2|x|
C.y=1-x2 D.y=x3-1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练D组练习卷(解析版) 题型:解答题
已知△ABC中,角A,B,C的对边分别为a,b,c,且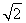 acos B=ccos B+bcos C.
acos B=ccos B+bcos C.
(1)求角B的大小;
(2)设向量m=(cos A,cos 2A),n=(12,-5),求当m·n取最大值时,tan C的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
P(x)=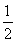 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
(1)写出第x月的需求量f(x)的表达式;
(2)若第x月的销售量g(x)=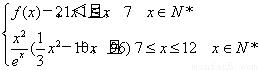
(单位:件),每件利润q(x)元与月份x的近似关系为:q(x)=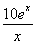 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=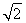 EF.
EF.
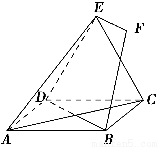
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练E组练习卷(解析版) 题型:填空题
若双曲线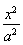 -
-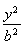 =1(a>0,b>0)与直线y=2x有交点,则离心率e的取值范围为________.
=1(a>0,b>0)与直线y=2x有交点,则离心率e的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练B组练习卷(解析版) 题型:填空题
若存在区间M=[a,b](a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”.给出下列四个函数:①y=ex,x∈R;②f(x)=x3;③f(x)=cos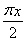 ;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com