B
分析:通过分类讨论将a
n=|2n-16|中的绝对值符号去掉,设{2n-16}的前n项和为S′
n,将问题转化为S
n=S′
n-2S′
8解使问题得到解决.
解答:∵a
n=|2n-16|,
∴当0<n≤8时,a
n=|2n-16|=16-2n,
当n>8时,a
n=|2n-16|=2n-16,
设{2n-16}的前n项和为S′
n,
则S
n=-(2×1-16)-(2×2-16)-(2×3-16)-…-(2×8-16)+(2×9-16)+…+(2n-16)
=-2[(2×1-16)+(2×2-16)+(2×3-16)+…+(2×8-16)]+[(2×1-16)+(2×2-16)+(2×3-16)+…+(2n-16)]
=S′
n-2S′
8=

-2×
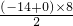
,
∵S
n=166,
∴n
2-15n+112=166,
∴n=18或n=-3(舍去).
故选B.
点评:本题考查数列的求和,过分类讨论将a
n=|2n-16|中的绝对值符号去掉是难点,考查转化思想与分类讨论思想的运用,属于中档题.

 -2×
-2×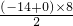 ,
,
