
【题目】已知双曲线![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,P为该双曲线上一点,满足
,P为该双曲线上一点,满足![]() ,P到坐标原点O的距离为d,且
,P到坐标原点O的距离为d,且![]() ,则
,则![]() ________.
________.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
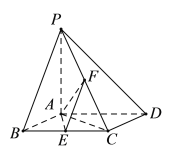
(I)证明:AE⊥PD;
(II)设AB=PA=2,
①求异面直线PB与AD所成角的正弦值;
②求二面角E-AF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,两个焦点分别是是
轴上的椭圆,两个焦点分别是是![]() ,
,![]() ,且
,且![]() ,
,![]() 是曲线上的任意一点,且点
是曲线上的任意一点,且点![]() 到两个焦点距离之和为4.
到两个焦点距离之和为4.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() :
:![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况,如三维饼图(2)所示.对比健身前后,关于这20名肥胖者,下面结论不正确的是( )
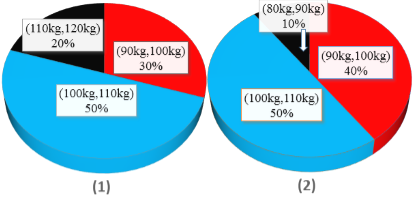
A.他们健身后,体重在区间![]() 内的人增加了2个
内的人增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.他们健身后,20人的平均体重大约减少了8 kg
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对于任意的正整数
满足:对于任意的正整数![]() ,
,![]() ,
,![]() ,且
,且![]() ,则称该数列为“跳级数列”.
,则称该数列为“跳级数列”.
(1)若数列![]() 为“跳级数列”,且
为“跳级数列”,且![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若数列![]() 为“跳级数列”,则对于任意一个大于
为“跳级数列”,则对于任意一个大于![]() 的质数
的质数![]() ,在数列
,在数列![]() 中总有一项是
中总有一项是![]() 的倍数;
的倍数;
(3)若![]() 为奇质数,则存在一个“跳级数列”
为奇质数,则存在一个“跳级数列”![]() ,使得数列
,使得数列![]() 中每一项都不是
中每一项都不是![]() 的倍数.
的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点![]() .
.
(1)求点P与抛物线C的焦点F的距离;
(2)设斜率为l的直线l与抛物线C交于A,B两点若△PAB的面积为![]() ,求直线l的方程;
,求直线l的方程;
(3)是否存在定圆M: ![]() ,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年初,某市为了实现教育资源公平,办人民满意的教育,准备在今年8月份的小升初录取中在某重点中学实行分数和摇号相结合的录取办法.该市教育管理部门为了了解市民对该招生办法的赞同情况,随机采访了440名市民,将他们的意见和是否近三年家里有小升初学生的情况进行了统计,得到如下的2×2列联表.
赞同录取办法人数 | 不赞同录取办法人数 | 合计 | |
近三年家里没有小升初学生 | 180 | 40 | 220 |
近三年家里有小升初学生 | 140 | 80 | 220 |
合计 | 320 | 120 | 440 |
(1)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关;
(2)从上述调查的不赞同小升初录取办法人员中根据近三年家里是否有小升初学生按分层抽样抽出6人,再从这6人中随机抽出3人进行电话回访,求3人中恰有1人近三年家里没有小升初学生的概率.
附:![]() ,其中
,其中![]() .
.
P( | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
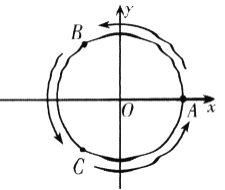
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
,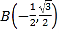 ,
,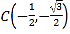 为圆上三个定点,某同学从
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为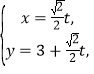 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com