
某公司计划2015年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元。甲、乙电视台的广告收费标准分别为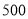 元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟。假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元。问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
公司在甲电视台做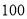 分钟广告,在乙电视台做
分钟广告,在乙电视台做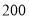 分钟广告,公司的收益最大,
分钟广告,公司的收益最大,
最大收益是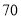 万元.
万元.
【解析】
试题分析:根据题意建立数学模型,设设公司在甲电视台和乙电视台做广告的时间分别为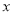 分钟和
分钟和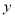 分钟,总收益为
分钟,总收益为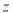 元,将实际问题转化关于线性规划的数学问题:即在约束条件
元,将实际问题转化关于线性规划的数学问题:即在约束条件 下求
下求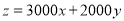 的最大值的线性规划问题,画出可行域,作出直线
的最大值的线性规划问题,画出可行域,作出直线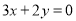 ,平行移动,当经过点
,平行移动,当经过点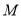
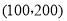 ,代入
,代入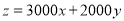 求得最大值收益是
求得最大值收益是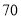 万元.
万元.
试题解析:设公司在甲电视台和乙电视台做广告的时间分别为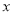 分钟和
分钟和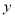 分钟,总收益为
分钟,总收益为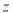 元, 2分
元, 2分
由题意得 6分
6分
目标函数为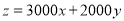 .7分
.7分
作出二元一次不等式组所表示的平面区域,即可行域.
如图所示: 10分
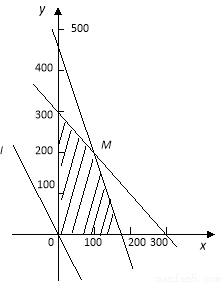
作直线 ,即
,即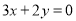 .
.
平移直线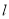 ,从图中可知,当直线
,从图中可知,当直线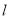 过
过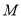 点时,目标函数取得最大值。
点时,目标函数取得最大值。
联立 解得
解得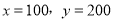 .
.
 点
点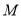 的坐标为
的坐标为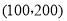 .
.
 (元) 13分
(元) 13分
答:该公司在甲电视台做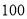 分钟广告,在乙电视台做
分钟广告,在乙电视台做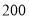 分钟广告,公司的收益最大,
分钟广告,公司的收益最大,
最大收益是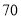 万元. 14分
万元. 14分
考点:1.数学模型;2.线性规划求最优解.


科目:高中数学 来源:2014-2015学年山西省大同市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知直线 (
( )与圆
)与圆 相切,则三条边长分别为
相切,则三条边长分别为 、
、 、
、 的三角形是
的三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第二段考文科数学卷(解析版) 题型:选择题
若双曲线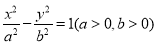 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的离心率是
,则该双曲线的离心率是
A.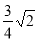 B.2 C.
B.2 C. D.
D.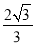
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省东莞市三校高二上学期期中联考试卷(解析版) 题型:选择题
△ABC中,AB=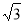 ,AC=1,∠B=30°则△ABC的面积等于 ( )
,AC=1,∠B=30°则△ABC的面积等于 ( )
A.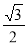 B.
B.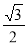 或
或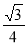 C.
C.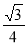 D.
D.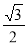 或
或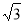
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上进教育名校学术联盟高三调研考试三文科数学试卷(解析版) 题型:选择题
若函数 对其定义域内的任意
对其定义域内的任意 ,当
,当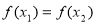 时,总有
时,总有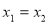 ,则称
,则称 为紧密函数.例如函数
为紧密函数.例如函数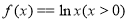 是紧密函数,下列命题:①紧密函数必是单调函数;②函数
是紧密函数,下列命题:①紧密函数必是单调函数;②函数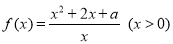 在
在 时是紧密函数;③函数
时是紧密函数;③函数 是紧密函数;④若函数
是紧密函数;④若函数 为定义域内的紧密函数,则
为定义域内的紧密函数,则 时,有
时,有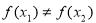 ;⑤若函数
;⑤若函数 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数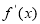 在定义域内的值一定不为零.其中的真命题是( )
在定义域内的值一定不为零.其中的真命题是( )
A.②④ B.①② C.①②④⑤ D.①②③⑤
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省枣庄市高三1月月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在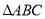 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足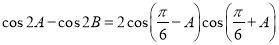
(1)求角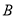 的值;
的值;
(2)若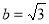 且
且 ,求
,求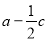 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com